Machine-translated from Chinese.
MV方法指用MV序列+五引理, 给出对开覆盖开集个数归纳的证明方法.
该方法导出若干重要的定理, 十分有用.
好覆盖的存在性
设$M$为$n$维流形, 其上开覆盖$\{U_\alpha\}$称为好覆盖,
若任意非空有限交微分同胚于$\mathbb{R}^n$.
定理 1.1. 流形具有好覆盖. 特别地, 紧流形有有限好覆盖.
证: 流形上可赋予黎曼度量(将$\mathbb{R}^n$上度量拉回,
再利用单位分解). 令$U_x$为$x$点测地凸邻域, 微分同胚于$\mathbb{R}^n$,
由于有限多个测地凸邻域非空交也是测地凸邻域,
从而$\{U_x\}_{x\in M}$是$M$的一个好的开覆盖.
测地凸邻域的概念可参考黎曼几何的教材.
称开覆盖$\mathcal U$为$\mathcal V$的加细, 若每个$U$包含在某个$V$中.
由于测地凸邻域可任意小, 容易证明每个开覆盖有一个加细的好覆盖.
de Rham上同调维数有限性
命题 1.1. 若$M$有有限好覆盖, 则$\dim H^\ast (M)<\infty$.
证: 记$h^q(M)=\dim H^q(M)$. 由MV序列,
$H^q(M)=H^q(U\cup V)\cong \ker r\oplus\operatorname{Im}r\cong \operatorname{Im}d^\ast \oplus \operatorname{Im}r$.
从而若$h^q(U), h^q(V), h^{q-1}(U\cap V)<\infty\Rightarrow h^q(U\cup V)<\infty$.
对有限好覆盖开集个数进行归纳, 当个数为 1 时, $M\approx \mathbb{R}^n$,
由 Poincaré 引理知结论成立.
归纳地, 假设流形具有开集个数不超过$p$个有限好覆盖时, 上同调维数有限.
若$M$具有有限好覆盖$\{U_0,...,U_p\}$. 取$W=U_0\cup ... \cup U_{p-1}$,
$V=U_p$.
则$W\cap V$有不超过$p$个的有限好覆盖$(\{U_0\cap U_{p},...,U_{p-1}\cap U_p\})$.
由归纳假设, $h^\ast (W\cap V), h^\ast (W), h^\ast (V)<\infty$,
从而$H^\ast (W\cup V)=H^\ast (M)<\infty$.
同理可证:
命题 1.2. 若$M$具有有限好覆盖, 则$\dim H_c^q(M)<\infty$.
定向流形的Poincaré对偶
设$V,W$为有限维向量空间,
设其间有配对$\left<{}-,-\right>:V\otimes_\mathbb{R}W\rightarrow \mathbb{R},$
为一个双线性映射, 则其诱导两个线性映射:
$$l_V:V\rightarrow W^\ast , v\mapsto \left<{}v,-\right>,$$
$$l_W:W\rightarrow V^\ast , w\mapsto \left<{}-,w\right>.$$
这里$V^\ast$, $W^\ast$指$V,W$的对偶空间. 若两诱导映射都是单射,
则称配对$\left<{},\right>$非退化.
引理 1.1. $\left<{}-,-\right>$非退化当且仅当诱导映射$l_V$为同构.
由于$V,W$都是有限维的, 做简单的泛函分析即可.
假定$M$为$n$维定向光滑流形, 具有有限好覆盖. 则$H^q(M)$,
$H^{n-q}_c(M)$为两个有限维向量空间.
定义配对$\int_M:H^1(M)\otimes_\mathbb{R}H^{n-q}_c(M)\rightarrow \mathbb{R}$,
$([\omega],[\tau])\mapsto \int_M \omega \wedge \tau$. 由Stokes定理,
该配对是良定的.
定理 1.2. 若$n$维定向光滑流形$M$有有限好覆盖, 则配对$\int_M$非退化, 等价地, 我们有$H^q(M)\cong (H^{n-q}_c(M))^\ast , H_c^{n-q}(M)\cong (H^q(M))^\ast$
证明前先做一些准备工作:
引理 1.2. 我们有如下带符号的交换图表, 如对最右侧的交换性, 即取$[\omega]\in H^q(U\cap V)$, $[\tau]\in H_c^{n-q-1}(U\cup V)$, 有$\int_{U\cup V}d^\ast \omega\wedge \tau=\pm \int_{U\cap V}\omega\wedge d_\ast \tau$.
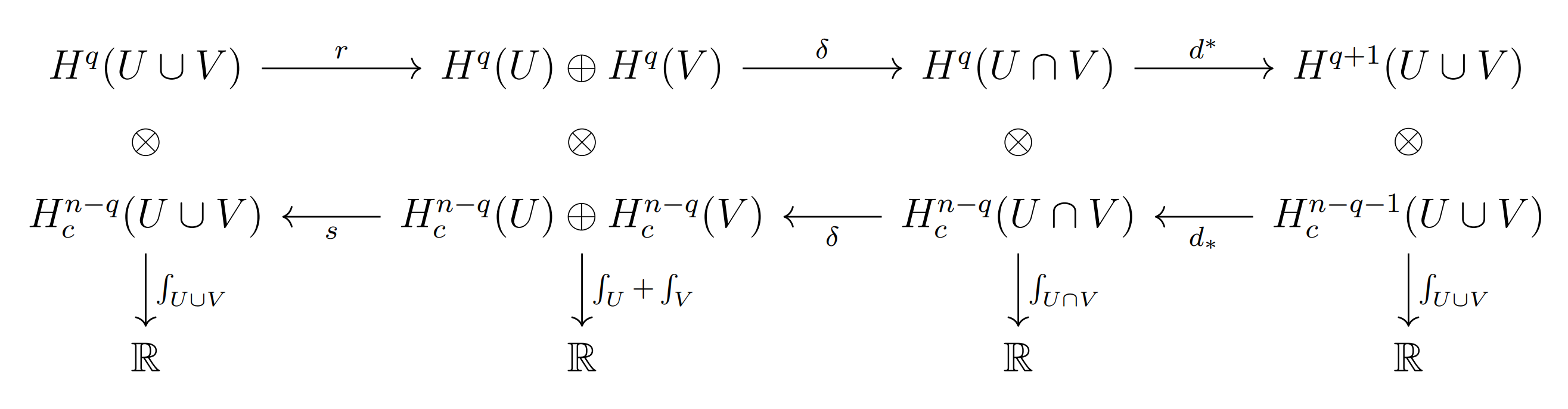
已经证明过$d^\ast ,d_\ast$与单位分解选取无关, 因此不妨用同一个单位分解,
将$d^\ast ,d_\ast$的映射具体地给出即可.
于是配对$\int$诱导了下面带符号的交换图表:
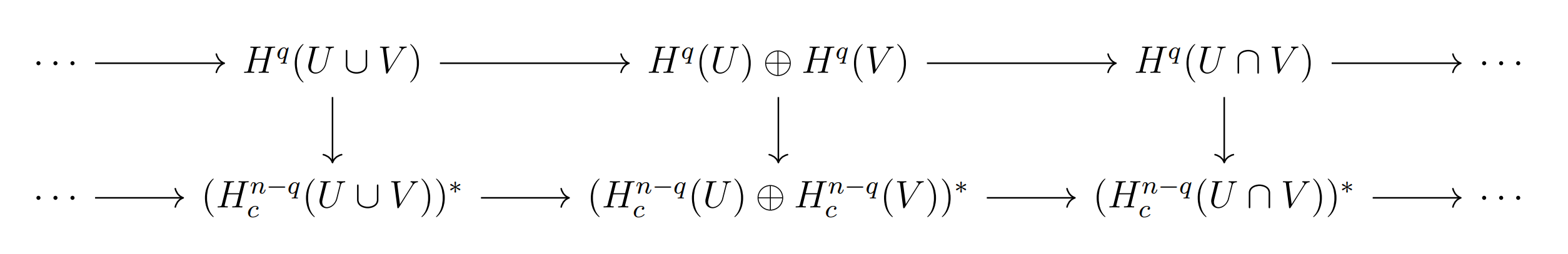
之后便可以借助五引理(Five Lemma)证明主命题了.
证: 由上正合列与五引理, 若 Poincaré 对偶在$U$, $V$, $U\cap V$上成立,
则在$U\cup V$上也成立.
对有限好覆盖开集个数归纳证明: 若仅有一个好覆盖, 由 Poincaré 引理得证.
若其对有限好覆盖开集个数不超过$p$的流形成立,
设$M$有好覆盖$\{U_0,...,U_p\}$, 令$W=U_0\cup ...\cup U_{p-1}$, $V=U_p$,
则$M,V,M\cap V$好覆盖开集数均不超过$p$,
从而$M=U\cup V$上成立Poincaré对偶.
若没有有限好覆盖, 则有如下定理:
定理 1.3. 若$M$为定向$n$维流形, 上同调不必是有限维的, 则:$H^q(M)\cong (H^{n-q}_c(M))^\ast$
也就是另一个同构关系不一定对, 因为直和的对偶是直积,
但直积的对偶不是直和. 如当$M$可被分解为$M=\sqcup_i M_i$,
可列个$M_i$每个均有有限开覆盖时, $H^k(M)=\prod_i H^k(M_i)$,
但$H_c^{k}(M)=\oplus_i H^{k}_c(M_i)$, 因为其需要具有紧支集.
那么此时$(H_c^{n-q}(M))^\ast =\prod(H_c^{n-q}(M_i))^\ast \cong \prod H^q(M_i)=H^q(M)$.
而另一个同构不一定成立.
由对偶关系, 即有:
推论 1.1. 若流形$M$连通可定向, 则$H^n_c(M)\cong \mathbb{R}$, 特别地, 若$M$还是紧的, 则$H^n(M)\cong \mathbb{R}$.
闭定向子流形的Poincaré对偶
设$M$为$n$维定向流形.
闭无边定向子流形
假设$S$为$M$的$k$维闭无边定向子流形, 考虑$\omega\in Z_c^k(M)$,
$\operatorname{supp}(i^\ast \omega)$也是$M$中的闭集,
从而$\operatorname{supp}(i^\ast \omega)\subset \operatorname{supp}\omega$紧,
$\int_Si^\ast \omega$有意义.
另一方面, $\,\forall\,\omega \in B_c^\ast (M)$, $\omega=d\phi$,
同理$\operatorname{supp}(i^\ast \phi)$紧. 进一步, 存在闭集$B$,
$\operatorname{supp}(i^\ast \phi)\subset B$且$\partial B$为光滑$k-1$维子流形或空集,
则由Stokes定理, $\int_Si^\ast \omega=\int_Bd(i^\ast \phi)=0$.
综上, $\int_S i^\ast$定义了$H_c^k(M)$上的一个线性泛函,
于是存在唯一的$[\eta_S]\in H^{n-k}(M)$,
$\int_S i^\ast \omega=\int_M\omega\wedge \eta_S$.
$[\eta_S]$或其任意代表元称为$S$的(闭)Poincaré对偶.
紧致无边定向子流形
当$S$紧时, 由于流形是$T_2$的, 当然$S$也是闭的, 上述讨论可以继承.
$\,\forall\,[\omega]\in H^k(M)$, 由紧性,
积分$\int_S i^\ast \omega$有意义. 此时它定义了$H^k(M)$上的一个线性泛函,
于是设$M$有有限好覆盖, 则便对应唯一的$[\eta_S']\in H^{n-k}_c(M)$,
满足$\int_Si^\ast \omega=\int_M \omega\wedge\eta_S'$.
$[\eta_S]$便称为$S$的紧Poincaré对偶.
容易看出自然映射$H_c^{n-k}(M)\rightarrow H^{n-k}(M)$把紧Poincaré对偶映为闭Poincaré对偶.
然而这两个可能有很大的区别, 如非零的紧Poincaré对偶可能被映为$0$.
局部化原理
取紧定向$k$维子流形$S$在$M$中的开邻域$W$, 即$S\subset W\subset M$,
那么将$S$在$W$中的紧Poincaré对偶零延拓到$M$上,
则容易验证它也是$M$中的紧Poincaré对偶.
这就是局部化原理:
$S$在$M$中紧Poincaré对偶的支集可缩小到$S$的任一开邻域中.
文章最后更新于 2021-09-21 17:25:28
The MV method refers to using the MV sequence + five lemmas to provide a proof method for the induction of the number of open sets that cover open sets.
This method derives several important theorems and is very useful.
Existence of Good Covers
Assume $M$ is a $n$-dimensional manifold, and the open cover $\{U_\alpha\}$ above it is called good coverage,
If any non-empty finite intersection diffeomorphism is in $\mathbb{R}^n$.
Theorem 1.1. Manifolds have good coverage. In particular, compact manifolds have finitely good coverage.
Certificate: A Riemannian metric can be assigned to the manifold (pull back the upper metric $\mathbb{R}^n$,
Then use partition of unity). Let $U_x$ be the geodesic convex neighborhood of $x$ point, and the diffeomorphism is $\mathbb{R}^n$,
Since the non-space intersection of a finite number of geodesic convex neighbors is also a geodesic convex neighborhood,
Therefore $\{U_x\}_{x\in M}$ is a good open cover of $M$.
For the concept of geodesic convex neighborhood, please refer to the textbook of Riemannian geometry.
The open coverage $\mathcal U$ is called $\mathcal V$ Add detail, if each $U$ is contained in some $V$.
Since the geodesic convex neighborhood can be arbitrarily small, it is easy to prove that every open cover has a thinned good cover.
de Rham cohomology finiteness
Proposition 1.1. If $M$ has finite good coverage, then $\dim H^\ast (M)<\infty$.
Certificate: Denote $h^q(M)=\dim H^q(M)$. From the MV sequence,
$H^q(M)=H^q(U\cup V)\cong \ker r\oplus\operatorname{Im}r\cong \operatorname{Im}d^\ast \oplus \operatorname{Im}r$.
So if $h^q(U), h^q(V), h^{q-1}(U\cap V)<\infty\Rightarrow h^q(U\cup V)<\infty$.
Summarize the number of finite well-covered open sets. When the number is 1, $M\approx \mathbb{R}^n$,
The conclusion is established by Poincaré’s lemma.
In summary, it is assumed that when the number of open sets of the manifold does not exceed $p$ finite good covers, the cohomology dimension is limited.
If $M$ has finite good coverage $\{U_0,...,U_p\}$. Take $W=U_0\cup ... \cup U_{p-1}$,
$V=U_p$.
Then $W\cap V$ has no more than $p$ finite good coverage $(\{U_0\cap U_{p},...,U_{p-1}\cap U_p\})$.
By the inductive hypothesis, $h^\ast (W\cap V), h^\ast (W), h^\ast (V)<\infty$,
Thus $H^\ast (W\cup V)=H^\ast (M)<\infty$.
The same principle can be proved:
Proposition 1.2. If $M$ has finite good coverage, then $\dim H_c^q(M)<\infty$.
Poincaré Duality of Oriented Manifolds
Let $V,W$ be a finite-dimensional vector space,
Assume there is a pair $\left<{}-,-\right>:V\otimes_\mathbb{R}W\rightarrow \mathbb{R},$
is a bilinear mapping, then it induces two linear mappings:
$$l_V:V\rightarrow W^\ast , v\mapsto \left<{}v,-\right>,$$
$$l_W:W\rightarrow V^\ast , w\mapsto \left<{}-,w\right>.$$
Here $V^\ast$, $W^\ast$ refer to the dual space of $V,W$. If both induced mappings are injective,
Then the pairing $\left<{},\right>$ is said to be non-degenerate.
Lemma 1.1. $\left<{}-,-\right>$ is non-degenerate if and only if the induced map $l_V$ is isomorphic.
Since $V,W$ is all finite-dimensional, simple functional analysis is enough.
Assume $M$ is a $n$-dimensional directional smooth manifold with finite good coverage. Then $H^q(M)$,
$H^{n-q}_c(M)$ is two finite-dimensional vector spaces.
Define pairing$\int_M:H^1(M)\otimes_\mathbb{R}H^{n-q}_c(M)\rightarrow \mathbb{R}$,
$([\omega],[\tau])\mapsto \int_M \omega \wedge \tau$. According to Stokes theorem,
The pairing is good.
Theorem 1.2. If the $n$-dimensional directional smooth manifold $M$ has finite good coverage, then the pairing $\int_M$ is non-degenerate. Equivalently, we have $H^q(M)\cong (H^{n-q}_c(M))^\ast , H_c^{n-q}(M)\cong (H^q(M))^\ast$
Do some preparatory work before proving:
Lemma 1.2. We have the following signed commutative diagram. For example, for the commutativity on the far right, we take $[\omega]\in H^q(U\cap V)$, $[\tau]\in H_c^{n-q-1}(U\cup V)$, and have $\int_{U\cup V}d^\ast \omega\wedge \tau=\pm \int_{U\cap V}\omega\wedge d_\ast \tau$.
It has been proved that $d^\ast ,d_\ast$ has nothing to do with the selection of partition of unity, so it may as well be decomposed with the same unit,
Just give the mapping of $d^\ast ,d_\ast$ specifically.
Then pairing $\int$ induces the following signed exchange graph:
Then we can use the Five Lemma to prove the main proposition.
Certificate: From the above exact sequence and the five lemmas, if the Poincaré duality holds on $U$, $V$, $U\cap V$,
Then it is also true on $U\cup V$.
Inductive proof for the number of finitely good covering open sets: If there is only one good covering, it is proved by Poincaré's lemma.
If it is established for a flow whose number of finitely well-covered open sets does not exceed $p$,
Assume $M$ has good coverage $\{U_0,...,U_p\}$, let $W=U_0\cup ...\cup U_{p-1}$, $V=U_p$,
Then the number of open sets covered by $M,V,M\cap V$ does not exceed $p$,
Therefore, the Poincaré duality is established on $M=U\cup V$.
If there is no finite good coverage, the following theorem follows:
Theorem 1.3. If $M$ is an oriented $n$-dimensional manifold, cohomology does not have to be finite-dimensional, then: $H^q(M)\cong (H^{n-q}_c(M))^\ast$
That is to say, another isomorphism relation is not necessarily correct, because the dual of a direct sum is a direct product,
But the dual of a direct product is not a direct sum. For example, when $M$ can be decomposed into $M=\sqcup_i M_i$,
When $M_i$ can be listed, each of them has limited open coverage, $H^k(M)=\prod_i H^k(M_i)$,
But $H_c^{k}(M)=\oplus_i H^{k}_c(M_i)$, because it needs to have compact support.
Then at this time $(H_c^{n-q}(M))^\ast =\prod(H_c^{n-q}(M_i))^\ast \cong \prod H^q(M_i)=H^q(M)$.
The other isomorphism may not be true.
From the duality relationship, we have:
Corollary 1.1. If the manifold $M$ is connected and orientable, then $H^n_c(M)\cong \mathbb{R}$. In particular, if $M$ is still compact, then $H^n(M)\cong \mathbb{R}$.
Poincaré duality of closed directed submanifolds
Let $M$ be the $n$-dimensional directional manifold.
Closed boundless directed submanifold
Assume $S$ is the $k$-dimensional closed boundless directed submanifold of $M$, consider $\omega\in Z_c^k(M)$,
$\operatorname{supp}(i^\ast \omega)$ is also a closed set in $M$,
Therefore $\operatorname{supp}(i^\ast \omega)\subset \operatorname{supp}\omega$ is tight,
$\int_Si^\ast \omega$ Makes sense.
On the other hand, $\,\forall\,\omega \in B_c^\ast (M)$, $\omega=d\phi$,
In the same way $\operatorname{supp}(i^\ast \phi)$ is compact. Further, there is a closed set $B$,
$\operatorname{supp}(i^\ast \phi)\subset B$ and $\partial B$ are smooth $k-1$-dimensional submanifolds or empty sets,
Then by Stokes theorem, $\int_Si^\ast \omega=\int_Bd(i^\ast \phi)=0$.
To sum up, $\int_S i^\ast$ defines a linear functional on $H_c^k(M)$,
So there is a unique $[\eta_S]\in H^{n-k}(M)$,
$\int_S i^\ast \omega=\int_M\omega\wedge \eta_S$.
$[\eta_S]$ or any of its representatives is called $S$ (Closed) Poincaré duality.
Compact boundless directed submanifold
When $S$ is compact, since the manifold is $T_2$, of course $S$ is also closed, and the above discussion can be inherited.
$\,\forall\,[\omega]\in H^k(M)$, due to compactness,
The integral $\int_S i^\ast \omega$ makes sense. At this time it defines a linear functional on $H^k(M)$,
So assuming $M$ has finite good coverage, it corresponds to the only $[\eta_S']\in H^{n-k}_c(M)$,
Satisfy$\int_Si^\ast \omega=\int_M \omega\wedge\eta_S'$.
$[\eta_S]$ is called $S$ Compact Poincaré duality.
It is easy to see that the natural mapping $H_c^{n-k}(M)\rightarrow H^{n-k}(M)$ maps the compact Poincaré duality into a closed Poincaré duality.
However, there may be a big difference between the two, for example, the non-zero compact Poincaré dual may be mapped as $0$.
localization principle
Take the open neighborhood $W$ of the compactly oriented $k$-dimensional submanifold $S$ in $M$, that is, $S\subset W\subset M$,
Then extend the compact Poincaré dual zero of $S$ in $W$ to $M$,
Then it is easy to verify that it is also the compact Poincaré dual in $M$.
this is localization principle:
$S$ The support of the compact Poincaré dual in $M$ can be reduced to any open neighborhood of $S$.
The article was last updated on 2021-09-21 17:25:28
