Machine-translated from Chinese.
Hausdorff测度
基本定义
本节假设$(X,d)$为度量空间.
记$\omega_m=\frac{\pi^{m/2} }{\Gamma(\frac{m}{2}+1)},$
其中$\Gamma(q)=\int_0^\infty t^{q-1}e^{-t}dt,$ $q>0.$
当$m\in \mathbb{Z}_+$时, $\omega_m$表示$m$维单位球$B_1^m(0)$体积.
对任意的$m\ge 0,$ 定义$m$维Hausdorff(外)测度为
$$\mathcal{H}^m(A)=\lim\limits_{\delta\rightarrow 0+}\mathcal{H}_\delta^m(A),\quad A\subset X,$$
其中$\mathcal{H}_\delta^m$称为$\mathcal{H}^m$的$\delta$逼近,
$\mathcal{H}_\delta^m(\varnothing):=0;$ $\,\forall\,$非空$A\subset X,$
$\mathcal{H}_\delta^m(A):=\omega_m\inf\sum_{j}\left(\frac{\operatorname{diam}C_j}{2}\right)^m,$
下确界在所有满足$C_1,\cdots\subset X,$ $\operatorname{diam}C_j<\delta,$
$A\subset \bigcup_j C_j$的集合列中取. 若找不到这样的集合列,
则视为$\inf \varnothing=+\infty.$
容易验证$\mathcal{H}_\delta^m$与$\mathcal{H}^m$都是外测度.
由于$H_\delta^m$关于$\delta$单减,
因此$\delta\rightarrow 0+$处的极限总存在(可能是$+\infty$),
故可记$\mathcal{H}^m(A)=\sup_{\delta>0}\mathcal{H}_\delta^m(A).$
容易验证$\mathcal{H}^m$与$\mathcal{H}_\delta^m$均是外测度.
注意到$\mathcal{H}^0$事实上即为计数测度.
注 1.1. 由于$\operatorname{diam}C=\operatorname{diam}\overline{C},$ 可额外要求$\mathcal{H}_\delta^m$中选取的集合为闭集. 由于闭集有小的开邻域, 也可选取开集. 对完全有界集$A,$ $\mathcal{H}_\delta^m(A)<\infty,$ $\,\forall\,m\ge0,$ $\delta>0.$
容易看出$\mathcal{H}^m$满足Caratheodory判别准则,
因此$\mathcal{H}^m$是Borel测度. 特别地由前面的注记,
容易说明它还是Borel正则测度. 不过需要注意的是,
$\mathcal{H}_\delta^m$不见得是Borel测度, 比如在$\mathbb{R}^2$上,
对$\mathcal{H}_1^1,$ 取$S_\frac{1}{2}=I\times \{0,\frac{1}{2}\},$
$I=[0,1].$ 那么$\mathcal{H}_1^1(S_\frac{1}{2})<2,$
但是对Borel集$\mathbb{H}=\{y>0\},$
$\mathcal{H}_1^1(S_\frac{1}{2}\cap \mathbb{H})=\mathcal{H}_1^1(S_\frac{1}{2}\setminus \mathbb{H})=1,$
因此$\mathbb{H}$不满足Caratheodory条件, 并不是$\mathcal{H}_1^1$-可测集.
几何意义
事实上, 对整数$m\ge 1,$
$\mathcal{H}^m$恰恰就是$\mathbb{R}^{n}$中$m$维$C^1$子流形的体积测度,
$n\ge m.$ 我们先说明$\mathcal{H}^n,\mathcal{L}^n$在$\mathbb{R}^n$上一致.
首先回忆$\mathcal{L}^n$的定义.
定义$\mathcal{K}$为全体$n$维开区间$I=(a_1,b_1)\times\cdots\times(a_n,b_n)$的集合.
定义开区间的体积$|I|=(b_1-a_1)\cdots(b_n-a_n).$
接下来定义$\mathcal{L}^n(A)=\inf\sum_j |I_j|,$
下确界在满足$\{I_j\}\in \mathcal{K},$
$A\subset\bigcup_jI_j$的集合列中取.
容易看出$\mathcal{L}^n$由具如下特征的外测度刻画:
$$\mu^n(I)=|I|,\,\forall\,I\in \mathcal{K},\quad \mu^n(A)=\inf_{\text{开}U\supset A}\mu^n(U),\,\forall\,A\subset \mathbb{R}^n.$$
这是因为由Caratheodory判别法, $\mu^n$是Borel(正则)测度,
因此由$\mathcal{K}$在可列并/交/补运算下生成的集合都是可测集.
$\mathcal{K}$在有限交下封闭, 由此不难证明对有限并,
有$\mu^n(\bigcup_jI_j)=\mathcal{L}^n(\bigcup_jI_j),$
进而由单调性对可列并也对. 而$\mathcal{K}$为拓扑基,
在可列并操作下生成全体开集,
因此$\mu^n(U)=\mathcal{L}^n(U)$对所有开集$U$成立,
进而由定义即有$\mu^n=\mathcal{L}^n.$
接下来我们证明$\mathcal{L}^n(A)=\mathcal{H}^n(A),$
事实上可以说明$\mathcal{L}^n(A)=\mathcal{H}_\delta^n(A),$ 为此首先说明:
引理 1.2. $\mathcal{H}_\delta^n(A)\le \mathcal{L}^n(A),$ $\,\forall\,\delta>0.$
证: 由Vitali/Besicovitch覆盖引理(下一节介绍), 对任意开集$U,$
可找到无交闭球族$\{B_j\},$ $\operatorname{diam}B_j<\delta,$
$B_j\subset U,$ $\mathcal{L}^n(U\setminus \bigcup_j B_j)=0.$
即闭球族在$\mathcal{L}^n$测度意义下覆盖$U.$
由定义容易看出$\mathcal{L}^n(A)=0\Leftrightarrow \mathcal{H}_\delta^n(A)=0,$
因此也有$\mathcal{H}_\delta^n(U\setminus \bigcup_j B_j)=0.$
取$U$为$I_k\in \mathcal{K}.$ 那么
$$\begin{aligned}
\mathcal{H}_\delta^n(I_k)&=\mathcal{H}_\delta^n(\cup_jB_j)\le\sum_j \omega_n\left(\frac{\operatorname{diam}B_j}{2}\right)^n\\
&=\sum_j\mathcal{L}^n(B_j)=\mathcal{L}^n(\cup_j B_j)=\mathcal{L}^n(I_k)=|I_k|.
\end{aligned}$$
进而$\,\forall\,A\subset \bigcup_k I_k,$
$$\mathcal{H}_\delta^n(A)\le\mathcal{H}_\delta^n(\cup_k I_k)\le \sum_k\mathcal{H}_\delta^n(I_k)\le \sum_k |I_k|.$$
对所有这样的$\{I_k\}$取下确界,
即可说明$\mathcal{H}_\delta^n(A)\le \mathcal{L}^n(A).$
为了说明反向的不等式, 首先需要如下定理:
定理 1.3 (等直径不等式). $\mathcal{L}^n(A)\le \omega_n\left(\frac{\operatorname{diam}A}{2}\right)^n.$
证: 只需证明$A$为紧集的情形,
因为$\operatorname{diam}A=\infty$时平凡(有界),
而$A\subset \overline{A},$
$\operatorname{diam}{\overline{A} }=\operatorname{diam}{A}$(闭).
对紧集$A,$ 我们做Steiner对称化: 在$x^j$方向,
对所有$j$分量为$0$的坐标点$\xi,$
截取$A$与从$\xi$点出发的$x^j$线$\ell_j(\xi)$相交的部分,
重置为相同长度的以$\xi$为中点, 落在$x^j$线上的线段, 如下图所示.
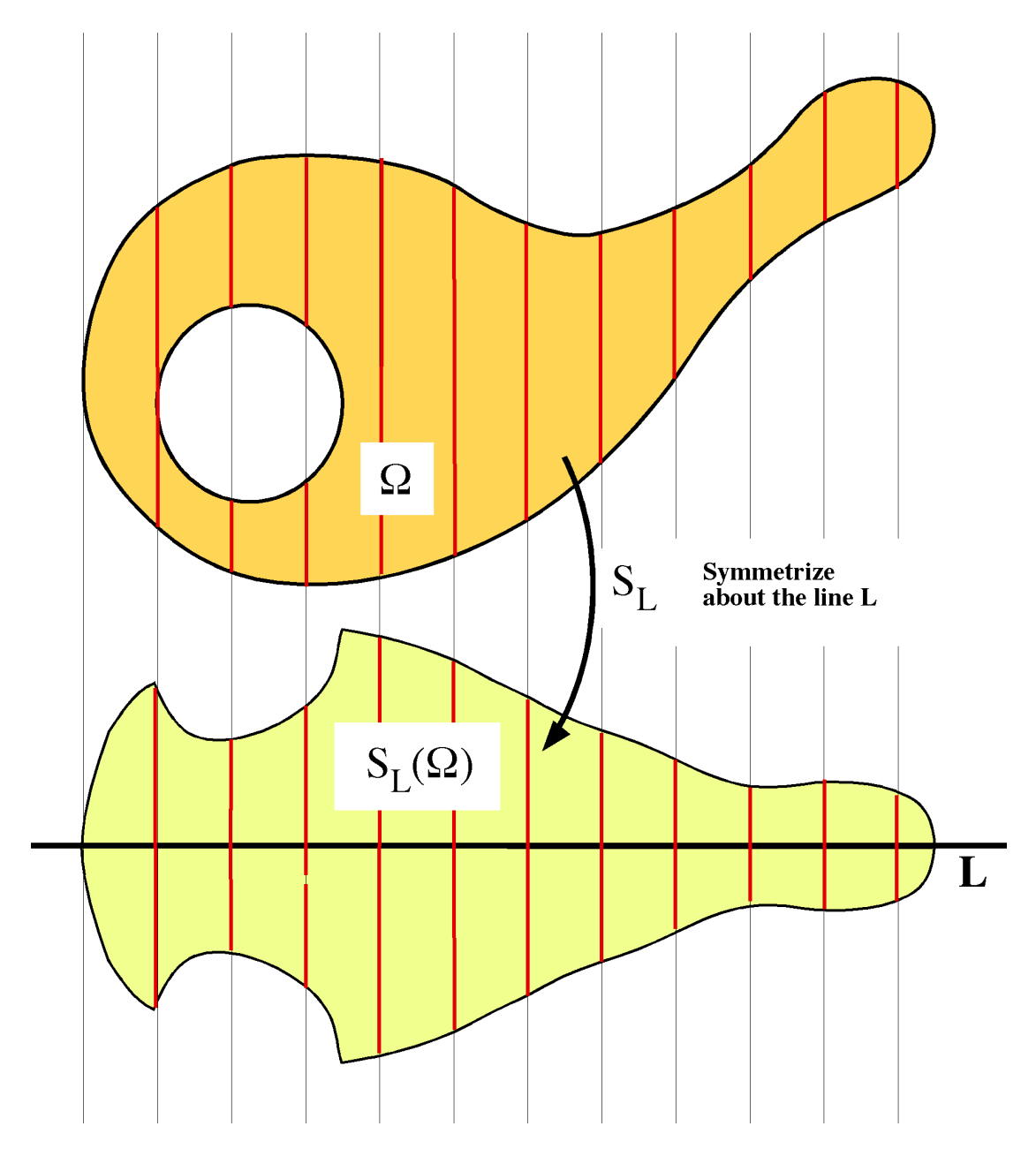
首先说明对称化后的集合是紧的, 这在后面说明直径减小时会用到.
只需说它是闭的. 记$A$在$\xi$点上$x^j$方向截取的长度为$2f(\xi),$
则$\,\forall\,\xi_i\rightarrow \xi,$ $t_i\rightarrow t,$
$|t_i|\le f(\xi_i),$ 需说明$|t|\le f(\xi).$ 只需说明$f$是上半连续的,
这样就有$f(\xi)\ge \varlimsup_i f(\xi_i)\ge \varlimsup_i |t_i|=|t|.$
记$\pi:\mathbb{R}^n\rightarrow \mathbb{R}$为到$x^j$方向上的投影,
那么$f(\xi)=\mathcal{L}^1(\pi(A\cap \ell_j(\xi))).$
$\,\forall\,\varepsilon>0,$
可以取开区间$U\supset\pi(A\cap \ell_j(\xi)),$
使得$\mathcal{L}^1(U)\le f(\xi)+\varepsilon.$
取开集$\pi^{-1}(U)\supset A\cap \ell_j(\xi),$
我们说明对充分靠近$\xi$的$\eta,$
有$A\cap\ell_j(\eta)\subset \pi^{-1}(U).$ 不然有$\xi_i\rightarrow \xi,$
使得$A\cap \ell_j(\xi_i)$中总有不在$\pi^{-1}(U)$中的点$x_i=\xi_i+s_i e_j,$
$s_i\in \mathbb{R}.$ 由于$A$有界, 有界点列$\{s_i=\pi(x_i)\}$有收敛子列,
不妨设自身收敛, 那么$x_i=\xi_i+s_i e_j\rightarrow \xi+s e_j=:x.$
由于$U^c$闭, $\pi(x)\notin U,$
但是$x\in A\cap \ell_j(\xi)\subset \pi^{-1}(U),$ 矛盾.
这样就说明$\,\exists\,\delta>0,$ $\,\forall\,\eta\in O_\delta(\xi),$
$f(\eta)\le f(\xi)+\varepsilon,$ 即$f$是上半连续的.
由Fubini定理, 对称化后$\mathcal{L}^n$测度不变,
而对称化后的直径比原先要小, 因此考虑对对称化后的情形证明即可.
直径减小是因为设对称化后$a,b$为$|b-a|$取到直径长度的两点,
那么他们关于$x^j=0$的对称点$\widetilde{a},\widetilde{b}$也是$|\widetilde{b}-\widetilde{a}|$取到直径长度的两点.
如果$a,b$在原集合中距离小于$|b-a|,$
那么$\widetilde{a},\widetilde{b}$在原集合中距离一定会放大.
这用勾股定理即可简单地说明.
容易证明对已经关于$x^i=0$对称的集合做$x^j$方向的Steiner对称化后,
仍是关于$x^i=0$对称的. 因此对$A$做所有$x^j$方向的Steiner对称化后,
它在所有$x^j$方向上对称, 特别地还是中心对称的. 记其为$\widetilde{A},$
那么它一定包含在以原点为球心,
$\operatorname{diam}\widetilde{A}$为直径的闭球内. 由此命题得证.
定理 1.4. $\mathcal{L}^n(A)=\mathcal{H}^n(A)=\mathcal{H}^n_\delta(A),$ $\,\forall\,A\subset \mathbb{R}^n, \delta>0.$
证: 由前面的引理,
只需再说明$\mathcal{L}^n(A)\le \mathcal{H}_\delta^n(A).$
而这由上面的不等式是即得的, 与引理证明方法相同.
即$\,\forall\,A\subset C_j,$
$$\mathcal{L}^n(A)\le \mathcal{L}^n(\cup_j C_j)\le \sum_j\mathcal{L}^n(C_j)\le \sum_j\omega_n\left(\frac{\operatorname{diam}C_j}{2}\right)^n.$$
那么对所有这样的$\{C_j\}$取下确界,
即有$\mathcal{L}^n(A)\le \mathcal{H}_\delta^n(A).$
文章最后更新于 2021-10-25 10:58:21
Hausdorff measure
basic definition
This section assumes that $(X,d)$ is a metric space.
Note$\omega_m=\frac{\pi^{m/2} }{\Gamma(\frac{m}{2}+1)},$
Among them $\Gamma(q)=\int_0^\infty t^{q-1}e^{-t}dt,$ $q>0.$
When $m\in \mathbb{Z}_+$, $\omega_m$ represents the $m$-dimensional unit sphere $B_1^m(0)$ volume.
For any $m\ge 0,$, define the $m$-dimensional Hausdorff (external) measure as
$$\mathcal{H}^m(A)=\lim\limits_{\delta\rightarrow 0+}\mathcal{H}_\delta^m(A),\quad A\subset X,$$
Where $\mathcal{H}_\delta^m$ is called $\delta$ approximation of $\mathcal{H}^m$,
$\mathcal{H}_\delta^m(\varnothing):=0;$ $\,\forall\,$ Not empty $A\subset X,$
$\mathcal{H}_\delta^m(A):=\omega_m\inf\sum_{j}\left(\frac{\operatorname{diam}C_j}{2}\right)^m,$
The lower bound satisfies all $C_1,\cdots\subset X,$ $\operatorname{diam}C_j<\delta,$
Take the set column of $A\subset \bigcup_j C_j$. If no such set column is found,
is regarded as $\inf \varnothing=+\infty.$
It is easy to verify that $\mathcal{H}_\delta^m$ and $\mathcal{H}^m$ are both external measures.
Since $H_\delta^m$ decreases with respect to $\delta$,
Therefore, the limit at $\delta\rightarrow 0+$ always exists (possibly $+\infty$),
Therefore, it can be remembered$\mathcal{H}^m(A)=\sup_{\delta>0}\mathcal{H}_\delta^m(A).$
It is easy to verify that $\mathcal{H}^m$ and $\mathcal{H}_\delta^m$ are both external measures.
Note that $\mathcal{H}^0$ is actually a counting measure.
Note 1.1. Since $\operatorname{diam}C=\operatorname{diam}\overline{C},$ can additionally require that the set selected in $\mathcal{H}_\delta^m$ be a closed set. Since a closed set has a small open neighborhood, an open set can also be selected. For completely bounded sets $A,$ $\mathcal{H}_\delta^m(A)<\infty,$ $\,\forall\,m\ge0,$ $\delta>0.$
It is easy to see that $\mathcal{H}^m$ satisfies the Caratheodory criterion,
Therefore $\mathcal{H}^m$ is the Borel measure. In particular, from the previous notation,
It is easy to show that it is still a Borel regular measure. However, it should be noted that,
$\mathcal{H}_\delta^m$ is not necessarily a Borel measure. For example, on $\mathbb{R}^2$,
Get $S_\frac{1}{2}=I\times \{0,\frac{1}{2}\},$ for $\mathcal{H}_1^1,$
$I=[0,1].$ Then $\mathcal{H}_1^1(S_\frac{1}{2})<2,$
But for the Borel set $\mathbb{H}=\{y>0\},$
$\mathcal{H}_1^1(S_\frac{1}{2}\cap \mathbb{H})=\mathcal{H}_1^1(S_\frac{1}{2}\setminus \mathbb{H})=1,$
Therefore $\mathbb{H}$ does not satisfy the Caratheodory condition and is not a measurable set $\mathcal{H}_1^1$.
Geometric meaning
In fact, for the integer $m\ge 1,$
$\mathcal{H}^m$ is exactly the volume measure of the $m$-dimensional $C^1$ submanifold in $\mathbb{R}^{n}$,
$n\ge m.$ Let us first explain that $\mathcal{H}^n,\mathcal{L}^n$ is consistent with $\mathbb{R}^n$.
First recall the definition of $\mathcal{L}^n$.
Define $\mathcal{K}$ as the set of all $n$-dimensional open intervals $I=(a_1,b_1)\times\cdots\times(a_n,b_n)$.
Define the volume of the open interval $|I|=(b_1-a_1)\cdots(b_n-a_n).$
Next define $\mathcal{L}^n(A)=\inf\sum_j |I_j|,$
The lower bound satisfies $\{I_j\}\in \mathcal{K},$
Take it from the set column of $A\subset\bigcup_jI_j$.
It is easy to see that $\mathcal{L}^n$ is characterized by an external measure with the following characteristics:
$$\mu^n(I)=|I|,\,\forall\,I\in \mathcal{K},\quad \mu^n(A)=\inf_{\text{开}U\supset A}\mu^n(U),\,\forall\,A\subset \mathbb{R}^n.$$
This is because according to the Caratheodory discriminant method, $\mu^n$ is the Borel (regular) measure,
Therefore, the sets generated by $\mathcal{K}$ under the computable union/intersection/complement operations are all measurable sets.
$\mathcal{K}$ is closed under finite union, so it is not difficult to prove that for finite union,
Yes $\mu^n(\bigcup_jI_j)=\mathcal{L}^n(\bigcup_jI_j),$
Furthermore, pairs of monotonicity can be combined into pairs. And $\mathcal{K}$ is a topological basis,
Generate all open sets under columnar and union operations,
Therefore $\mu^n(U)=\mathcal{L}^n(U)$ holds for all open sets $U$,
Then from the definition $\mu^n=\mathcal{L}^n.$
Next we prove that $\mathcal{L}^n(A)=\mathcal{H}^n(A),$
In fact, it can be explained $\mathcal{L}^n(A)=\mathcal{H}_\delta^n(A),$. For this reason, first of all:
Lemma 1.2. $\mathcal{H}_\delta^n(A)\le \mathcal{L}^n(A),$ $\,\forall\,\delta>0.$
Certificate: By the Vitali/Besicovitch covering lemma (introduced in the next section), for any open set $U,$
A family of unintersecting closed spheres can be found $\{B_j\},$ $\operatorname{diam}B_j<\delta,$
$B_j\subset U,$ $\mathcal{L}^n(U\setminus \bigcup_j B_j)=0.$
That is, the closed sphere family covers $U.$ in the sense of $\mathcal{L}^n$ measure.
It is easy to see from the definition $\mathcal{L}^n(A)=0\Leftrightarrow \mathcal{H}_\delta^n(A)=0,$
Therefore there is also $\mathcal{H}_\delta^n(U\setminus \bigcup_j B_j)=0.$
Take $U$ as $I_k\in \mathcal{K}.$ then
$$\begin{aligned}
\mathcal{H}_\delta^n(I_k)&=\mathcal{H}_\delta^n(\cup_jB_j)\le\sum_j \omega_n\left(\frac{\operatorname{diam}B_j}{2}\right)^n\\
&=\sum_j\mathcal{L}^n(B_j)=\mathcal{L}^n(\cup_j B_j)=\mathcal{L}^n(I_k)=|I_k|.
\end{aligned}$$
Then $\,\forall\,A\subset \bigcup_k I_k,$
$$\mathcal{H}_\delta^n(A)\le\mathcal{H}_\delta^n(\cup_k I_k)\le \sum_k\mathcal{H}_\delta^n(I_k)\le \sum_k |I_k|.$$
Determine all such $\{I_k\}$,
Just explain $\mathcal{H}_\delta^n(A)\le \mathcal{L}^n(A).$
In order to explain the reverse inequality, we first need the following theorem:
Theorem 1.3 (equal diameter inequality). $\mathcal{L}^n(A)\le \omega_n\left(\frac{\operatorname{diam}A}{2}\right)^n.$
Certificate: Just prove that $A$ is a compact set,
Because $\operatorname{diam}A=\infty$ is trivial (bounded),
And $A\subset \overline{A},$
$\operatorname{diam}{\overline{A} }=\operatorname{diam}{A}$(closed).
For compact sets $A,$ we do Steiner symmetrization: In the $x^j$ direction,
For all coordinate points $\xi,$ whose $j$ component is $0$
Cut off the part where $A$ intersects with the $x^j$ line $\ell_j(\xi)$ starting from the point $\xi$,
Reset to a line segment of the same length with $\xi$ as the midpoint and falling on the $x^j$ line, as shown in the figure below.
First, explain that the symmetrized set is compact, which will be used later when explaining the diameter reduction.
Just say that it is closed. Note that the length of $A$ intercepted in the $x^j$ direction at the $\xi$ point is $2f(\xi),$
Then $\,\forall\,\xi_i\rightarrow \xi,$ $t_i\rightarrow t,$
$|t_i|\le f(\xi_i),$ Need to explain $|t|\le f(\xi).$ Just explain that $f$ is upper semi-continuous,
This way we have $f(\xi)\ge \varlimsup_i f(\xi_i)\ge \varlimsup_i |t_i|=|t|.$
Let $\pi:\mathbb{R}^n\rightarrow \mathbb{R}$ be the projection in the $x^j$ direction,
Then $f(\xi)=\mathcal{L}^1(\pi(A\cap \ell_j(\xi))).$
$\,\forall\,\varepsilon>0,$
You can take the open interval $U\supset\pi(A\cap \ell_j(\xi)),$
Make$\mathcal{L}^1(U)\le f(\xi)+\varepsilon.$
Take the open set$\pi^{-1}(U)\supset A\cap \ell_j(\xi),$
We show that $\eta,$ is sufficiently close to $\xi$
There is $A\cap\ell_j(\eta)\subset \pi^{-1}(U).$, otherwise there is $\xi_i\rightarrow \xi,$
So that there is always a point $x_i=\xi_i+s_i e_j,$ in $A\cap \ell_j(\xi_i)$ that is not in $\pi^{-1}(U)$
$s_i\in \mathbb{R}.$ Since $A$ is bounded, the bounded point sequence $\{s_i=\pi(x_i)\}$ has a convergent subsequence,
Let’s assume that it converges by itself, then $x_i=\xi_i+s_i e_j\rightarrow \xi+s e_j=:x.$
Since $U^c$ is closed, $\pi(x)\notin U,$
But $x\in A\cap \ell_j(\xi)\subset \pi^{-1}(U),$ is contradictory.
This means $\,\exists\,\delta>0,$ $\,\forall\,\eta\in O_\delta(\xi),$
$f(\eta)\le f(\xi)+\varepsilon,$ That is, $f$ is upper semi-continuous.
According to Fubini’s theorem, the $\mathcal{L}^n$ measure remains unchanged after symmetry,
The diameter after symmetrization is smaller than the original, so just consider the case after symmetry to prove it.
The diameter decreases because assuming that $a,b$ is $|b-a|$ after symmetry, two points of the diameter length are obtained,
Then their symmetry point $\widetilde{a},\widetilde{b}$ about $x^j=0$ is also the two points where the diameter length of $|\widetilde{b}-\widetilde{a}|$ is taken.
If $a,b$ is less than $|b-a|,$ in the original set
Then the distance of $\widetilde{a},\widetilde{b}$ in the original set will definitely be enlarged.
This can be simply explained using the Pythagorean theorem.
It is easy to prove that after performing Steiner symmetrization in the $x^j$ direction on a set that is already symmetric about $x^i=0$,
It is still symmetric about $x^i=0$. Therefore, after doing Steiner symmetrization on $A$ in all $x^j$ directions,
It is symmetrical in all $x^j$ directions, especially centrally symmetrical. Mark it as $\widetilde{A},$
Then it must be included in the sphere with the origin as the center,
$\operatorname{diam}\widetilde{A}$ is inside a closed sphere with diameter. This proposition is proved.
Theorem 1.4. $\mathcal{L}^n(A)=\mathcal{H}^n(A)=\mathcal{H}^n_\delta(A),$ $\,\forall\,A\subset \mathbb{R}^n, \delta>0.$
Certificate: From the previous lemma,
Just explain $\mathcal{L}^n(A)\le \mathcal{H}_\delta^n(A).$
And this is obtained immediately from the above inequality, which is the same as the lemma proof method.
That is $\,\forall\,A\subset C_j,$
$$\mathcal{L}^n(A)\le \mathcal{L}^n(\cup_j C_j)\le \sum_j\mathcal{L}^n(C_j)\le \sum_j\omega_n\left(\frac{\operatorname{diam}C_j}{2}\right)^n.$$
Then delimit all such $\{C_j\}$,
That is $\mathcal{L}^n(A)\le \mathcal{H}_\delta^n(A).$
The article was last updated on 2021-10-25 10:58:21
