Machine-translated from Chinese.
置换群
回忆对称群的任意子群称为置换群(permutation group),
图的自同构群是一个置换群. 群$G$的一个置换表示(permutation
representation)指$G$到某对称群$\operatorname{Sym}(V)$的同态,
也称为群$G$在集合$V$上的作用(action).
一个表示是忠实的(faithful)若它是单射, 仅将单位元映至恒等置换.
群$G$在集合$V$上的作用也诱导了其它的作用,
如其在集合$V$幂集$2^V$上的作用, 给出了子集间的置换.
注意到作用保子集大小, 因此也可以作用在$V$的$k-$子集全体上,
或将子集改为有序元组.
称集合$V$子集$S$是$G-$不变的, 若$\,\forall\,s\in S, g\in G,$
$s^g\in S.$ 此时任意$g\in G$给出$S$中元素的置换,
可以将其限制在$S$上, 记为$g|_S.$ 限制置换全体记为$G|_S,$ 或$G^S.$
$G$在$V$上的作用是可迁(transitive)的, 若任意给定$x,y\in V,$
存在$g\in G$使得$x^g=y.$
$G-$不变子集$S$称为轨道(orbit)若$G|_S$在$S$上是可迁的.
$\,\forall\,x\in V,$ $x^G:=\{x^g:g\in G\}$是一个轨道.
轨道彼此不相交, 给出了$V$的一个划分. 每个元素恰落在一个轨道里.
每个$G-$不变子集都是一系列轨道的并, 因此也可以称轨道为极小$G-$不变子集.
计数
令$G$为$V$的置换群, $\,\forall\,x\in V,$
稳定子(stabilizer)$G_x$为使得$x^g=x$的全体置换, 形成一个子群.
给定$S=\{x_1,\cdots,x_r\}\subset V,$
逐点稳定子$G_{x_1,\cdots,x_r}:=\bigcap_{i=1}^r G_{x_i},$
集合稳定子$G_S$为仅要求$S^g=S$的全体置换. 易见前者为后者子群.
引理 1.1. 设$G$作用在$V$上, $S$为$G$的轨道. 若$x,y\in S,$ 那么将$x$映至$y$的所有置换为$G_x$的某个右陪集. 反过来$G_x$的右陪集中所有置换将$x$映至$S$中同一点.
本节证明基本为抽象代数基本练习, 在此均略过.
引理 1.2 (轨道稳定集定理). $|G_x||x^G|=|G|.$
取$h\in G,$ 称形如$g^{-1}hg$的元素与$h$共轭,
与$h$共轭的元素全体称为$h$的共轭类.
映射$\tau_g:h\rightarrow g^{-1}hg$给出了$G$的置换,
因此$G$在自身上有一个共轭作用, 以共轭类为轨道. 若$H$为$G$的子群,
则$g^{-1}Hg$也是子群, 称其与$H$共轭.
引理 1.3. 设$G$在$V$上有一个作用, 则$\,\forall\,x\in V, g\in G,$ $g^{-1}G_x g=G_{x^g}.$
记$\operatorname{fix}(g)$表示置换$g$下不动点个数, 熟知有如下引理:
引理 1.4 (Burnside). $G$作用在$V$上的轨道数等于$G$中元素不动点个数的平均值.
非对称图
图是非对称(asymmetric)的, 若其自同构群平凡.
本节我们证明几乎所有图都是非对称的, 即对于$n$个点的图,
非对称图的占比当$n\rightarrow \infty$时趋近于$1.$
设$V$含$n$个点, 记$K_V$为$n$个点的完全图.
所有含$n$个点的图均由$K_V$通过删边得到, 因此共有$2^{\binom{n}{2} }$个图,
与$E(K_V)$子集一一对应.
给定图$X,$ 与其同构的图全体称为$X$的同构类. 回忆同构定义,
可以看出同构类即为对称群$\operatorname{Sym}(V)$在$E(K_V)$幂集上作用的轨道.
由轨道稳定集定理, 有如下引理:
引理 1.5. 含$X$的同构类大小为$\frac{n!}{|\operatorname{Aut}(X)|}.$
由Burnside引理, 我们对同构类进行计数.
设置换$g$(生成的子群)作用在$E(K_V)$上有$r$个轨道,
记为$\operatorname{orb}_2(g)=r.$ 那么$g$作用在$E(K_V)$幂集上时,
这些轨道就是全部的极小$g-$不动点, 组合起来共有$2^r$个不动点.
从而图的同构类个数共有$\frac{1}{n!}\sum_{g\in \operatorname{Sym}(V)}2^{\operatorname{orb}_2(g)}$个.
如果所有图都是非对称的, 那么每个等价类里含$n!$个图,
因此有$\frac{2^{\binom{n}{2} } }{n!}$个等价类.
接下来我们说明事实上当$n\rightarrow \infty$时, 等价类数量趋于该值,
进而推断出几乎所有的图都是非对称的.
引理 1.6. 含$n$个顶点的图的同构类数量至多有$(1+o(1))\frac{2^{\binom{n}{2} } }{n!}$个.
证: 称某个置换无法固定的点全体为置换的支撑,
即置换的作用仅在支撑上体现. 断言对于所有支撑大小为$2r$的置换,
$\operatorname{orb}_2$最大值由以$r$个对换组成的置换实现.
边$xy$非置换的不动点当且仅当$x,y$均在支撑里且不在同一对换内,
或一者在支撑里, 另一者不在. 设置换中含$k$个对换,
那么不动的边共有$\binom{n-2r}{2}+k$条, 每条边都是单独的一个轨道.
对于在动的边, 直接考虑轨道数: 一者在支撑里,
另一者不在的边贡献的轨道数至多为$(n-2r)(k+2(r-k)/3)=(n-2r)(2r+k)/3$条;
均在支撑里且不在同一对换内的轨道数至多有$2k\cdot 2(r-k)/3+k(k-1)+\binom{2(r-k)}{2}/3=4/3 \cdot k(r-k)+k(k-1)+(r-k)(2r-2k-1)/3=[2r^2+k^2-r-2k]/3.$
与前面的合计至多共$\binom{n-2r}{2}+[r(2n-2r-1)+k(k+n-2r+1)]/3$条,
在$k=r$处达到最大值$(n-2r)(n-2r-1)/2+nr-r^2=n^2/2-rn+r^2-n/2+r=\binom{n}{2}+r(r-n+1).$
而对由$k=r$个对换组成的置换,
前面的轨道数只对$r-k$部分(非对换部分)进行了放缩估计, 因此当$k=r$时,
计算是精确的,
因此$\operatorname{orb}_2$最大值确实由以$r$个对换组成的置换实现,
且具体取值已经给出.
注意轨道数最大估计对支撑大小非偶数的置换也成立,
即将$2r$换为支撑大小$t\in[2,n]$(此时最大估计未必实现).
那么轨道数最大估计$\varphi(t)=\binom{n}{2}+\frac{t}{2}(\frac{t}{2}-n+1)$为二次函数,
以$t=n-1$为对称轴.
取$m\le n-2,$ 现将$\operatorname{Sym}(V)$划分为三类: 恒等变换,
支撑大小不超过$m$的置换与剩余的置换.
它们的大小分别不超过$1,\binom{n}{m}m!<n^m, n!<n^n.$ 由轨道数最大估计,
每个第二类置换轨道数至多有$\binom{n}{2}-(n-2)$个,
每个第三类置换轨道数至多有$\binom{n}{2}-\frac{m}{2}(n-\frac{m}{2}-1)\le \binom{n}{2}-\frac{nm}{4}$个.
从而图的同构类个数至多有$\frac{1}{n!}[2^{\binom{n}{2} }+n^m2^{\binom{n}{2}-(n-2)}+n^n2^{\binom{n}{2}-\frac{nm}{4} }]=\frac{2^{\binom{n}{2} } }{n!}(1+n^m2^{-(n-2)}+n^n2^{-\frac{nm}{4} }).$
记$n^m2^{-(n-2)}+n^n2^{-\frac{nm}{4} }=2^{m\log_2 n-(n-2)}+2^{n\log_2 n-\frac{nm}{4} },$
发现对足够大的$n,$ 取$m=\lceil 8log_2 n\rceil$, 即有该项为无穷小量.
因此同构类数量至多有$(1+o(1))\frac{2^{\binom{n}{2} } }{n!}$个.
推论 1.7. 几乎所有图都是非对称的.
证: 假设在所有同构类中, 非对称图的同构类占比为$\mu.$
每个非对称图所在同构类中含$n!$张图,
而其余同构类中至多含$\frac{n!}{2}$张图.
因此同构类平均大小至多为$\mu n!+(1-\mu) \frac{n!}{2}=(1+\mu) \frac{n!}{2}.$
而每个图当然在某个同构类里出现过,
因此$(1+\mu)\frac{n!}{2}(1+o(1))\frac{2^{\binom{n}{2} } }{n!}\ge 2^{\binom{n}{2} },$
$(1+\mu)(1+o(1))\ge 2.$ 从而当$n\rightarrow\infty$时,
$\mu\rightarrow 1.$
因此, 若将所有同构的图视为同一张图, 几乎所有图都是非对称的.
若将同构类里每张图都视作不同的图, 由于非对称图所在同构类里含图数量最多,
我们仍然得到几乎所有图都是非对称的.
对上的轨道
设$G$在$V$上有一个可迁作用, 它在$V\times V$上也自然有一个作用,
我们研究其上的轨道. 由于$G$是可迁的, $\{(x,x):x\in V\}$是一个轨道,
称为对角轨道. 设$\Omega\subset V\times V,$
记其转置$\Omega^T$为$\{(y,x):(x,y)\in \Omega\}.$
易见$\Omega^T$是$G-$不变的当且仅当$\Omega$也是. 若$\Omega$为轨道,
那么$\Omega=\Omega^T$或无交. $\Omega=\Omega^T$时称其为对称轨道.
引理 1.8. 设$G$在$V$上有一个可迁作用, $x\in V,$ 那么$G$在$V\times V$上的轨道与$G_x$在$V$上轨道一一对应.
证明为抽代练习, 在此略过.
因此$G$在$V\times V$上的轨道$\Omega$与$G_x$在$V$上的轨道联系.
称$G_x$在$V$上的轨道数为$G$的秩. 若$\Omega$对称,
称$G_x$在$V$上对应轨道是自配对(self-paired)的.
每个$V\times V$上的轨道$\Omega$可看为以$V$为顶点集,
$\Omega$为弧集的有向图, 当$\Omega$对称时为无向图.
注意当$\Omega$非对称时, 两点间仅有一条弧, 称其为定向图(oriented
graph).
引理 1.9. 令$G$为$V$上的可迁置换群, $\Omega$为$V\times V$上轨道. 设$(x,y)\in \Omega,$ 则$\Omega$对称当且仅当$\,\exists\,g\in G,$ 使得$(x^g,y^g)=(y,x).$
若$g$交换$x,y,$ 则对换$(xy)$在$g$中, 那么$g$为偶数阶, 从而$G$也是偶数阶.
称$G$在$V$上慷慨可迁(generously transitive), 若任意给定$x,y\in V,$
存在置换交换它们. $V\times V$上所有轨道都是对称的当且仅当$G$慷慨可迁.
每个$V\times V$上的轨道给出一个图, $G$中元素均是该图的自同构,
且作用在顶点集和边集上都是可迁的. 对于若干轨道之并,
$G$中元素也均为该图的自同构, 但仅作用在顶点集上可迁的.
注意$G$并不一定就是图的自同构群. 书中给出了$G=S_7,$ 可生成$J(7,3,1),$
但$S_8\subset \operatorname{Aut}(J(7,3,1))$的例子, 在此略过.
本原性
令$G$可迁作用在$V$上, 非空子集$S\subset V$称为$G$的非本源区块(block of
imprimitivity), 若$\,\forall\,g\in G,$
$S^g=S$或$S^g\cap S=\varnothing.$ 由于$G$可迁,
$S$的所有转换构成了$V$的划分.
这些不同转换构成的集合称为$G$的非本原系统.
如下图中, 正方体$Q$的自同构群作用在顶点集上是可迁的, 考虑距离易见,
所有相同颜色的点的集合都是非本原区块,
而四个集合构成了自同构群的非本原系统.
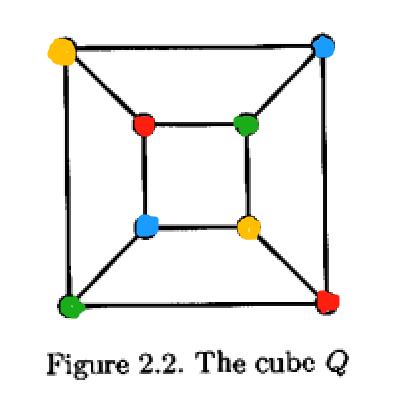
除了$S$为单点和全集的情况, 其余非本原系统都称为非平凡的.
若群没有非平凡非本原系统, 则称群是本原(primitive)的,
否则即为非本原的.
引理 1.10. $G$可迁作用在$V$上, $x\in V.$ $G$是本原的当且仅当$G_x$为$G$的极大子群.
证: 我们来证明$G$有非平凡非本原系统当且仅当$G_x$不是$G$的极大子群.
设$G$有非平凡非本原系统, 令$x\in B,$ $B$为一个非本原区块.
下面证明$G_x\subsetneq G_B\subsetneq G.$ 由于$\,\forall\,g\in G_x,$
$x\in B\cap B^g,$ 因此$B=B^g,$ $g\in G_B.$ 取$B$中另一元素$y\neq x.$
由可迁性存在$h\in G$使得$y=x^h.$ 从而$y\in B\cap B^h,$ $B=B^h,$
$h\in G_B.$ 然而$h\notin G_x,$ 从而$G_x$真包含于$G_B.$
设$G_x\subsetneq H\subsetneq G,$
我们说明$H$的轨道就是$G$的非平凡非本原系统. 记$B$为$H$含$x$的轨道,
取$g\in G,$ 需证明要么$B=B^g,$ 要么$B\cap B^g=\varnothing.$
假设$y\in B\cap B^g,$ 由于$x,y$同在轨道$B$内, $\,\exists\,h\in H,$
使得$y=x^h.$ 而由于$y\in B^g,$ 有$B$中元素$x^{h'},$ $x^{h'g}=y.$
因此$x^{h'gh^{-1} }=x,$ $h'gh^{-1}\in G_x\subsetneq H,$ 从而$g\in H.$
由于$B$是$H$的轨道, 即有$B=B^g.$
由于$G_x\subsetneq H,$ $B$不止由$x$组成. 为了说明$H$的轨道不是整个$V,$
回忆 $\,\forall\,y\in V,$ $G$将$x$映至$y$的所有置换为$G_x$某个右陪集.
若$H$也是可迁的, 则有$G_x H\supset G.$ 然而$G_x H=H$, 因此$H=G,$
与$H$为真子群矛盾. 从而$B\neq V$, 即$B$是非平凡的非本原系统.
本原性与连通性
关于本原性的另一个描述在$G$作用于$V\times V$的轨道上体现.
我们先做些预备工作.
有向图的一个路指不同顶点构成的序列$\{u_0,\cdots,u_r\},$
$(u_{i-1},u_i)$为弧; 有向图的弱路(weak
path)只要求$(u_{i-1},u_i)$或$(u_{i},u_{i-1})$为弧即可.
有向图是强连通的, 若任意两点有路径连接;
称其弱连通即指任意两点有弱路连接.
有向图的弱连通性即为无视方向后无向图的连通性. 有向图的强连通分支,
指强连通的极大诱导子图. 根据定义, 单点即为强连通的,
因此强连通分支构成了图的一个划分.
有向图中顶点的入度(in-valency)为以该点为终点的弧的个数;
出度(out-valency)即为以该点为起点的弧的个数.
引理 1.11. 若$D$为所有点出度与入度相同的有向图, 则$D$强连通当且仅当它弱连通.
证: 只需证明当$D$弱连通时, 它也是强连通的. 不然,
$D$可拆分为强连通分支$D_1,\cdots,D_r.$ 若有一条弧从$D_i$出发至$D_j,$
那么连接$D_i,D_j$的所有的弧都必须从$D_i$出发,
不然$D_i,D_j$可合并为强连通子图.
以$D$的强连通分支为顶点作有向图$D',$
$D_i$到$D_j$连有向边当且仅当$D$中存在一条弧从$D_i$出发至$D_j.$
由于$D$是弱连通的, $D'$也是. $D'$中不能出现环,
不然环涉及的强连通分支全体之并为强连通的.
从而易证$D'$中至少有一个点入度为零, 不妨设其对应强连通分支$D_1.$
对于涉及$D_1$的全体弧, 若其终点在$D_1$内, 起点必在$D_1$内,
出度与入度相消; 但是至少有一条边, 从$D_1$出发, 终点在$D_1$外,
因为$D'$是弱连通的. 因此$D_1$内全体点出度之和必定大于入度, 与条件矛盾.
回忆$G$可迁作用在$V$上时, $V\times V$上的轨道$\Omega$可视为有向图.
当$\Omega$非对称时, 图为定向图. 由于$G$是可迁的, 全体点出度相同,
入度相同. 又由于出度和等于入度和(等于弧数), 全体点出度等于入度.
因此轨道对应的有向图强连通性等于弱连通性, 泛称为轨道的连通性.
引理 1.12. $G$可迁作用在$V$上. $G$是本原的当且仅当每个非对角轨道连通.
证: 假设$G$是非本原的, $B_1,\cdots, B_r$为非本原系统.
设$x\neq y\in B_1,$ $\Omega$为$V\times V$上含$(x,y)$的轨道. 对$g\in G,$
$x^g,y^g$在相同非本原区块内. 从而$\Omega$的每条弧起终点都在同一区块内,
显然不连通.
反之设$\Omega$某一轨道不连通, $B$为$\Omega$某一连通分支的顶点全体.
这时$\,\forall\,g\in G,$ $B^g$显然也是连通的,
因此$B^g=B$或$B^g\cap B=\varnothing.$ 因此$B$为非本原区块,
$G$是非本原的.
文章最后更新于 2021-09-16 14:51:49
permutation group
Recall that any subgroup of a symmetric group is called permutation group,
The automorphism group of a graph is a permutation group. A member of the group $G$ permutation
representation) Refers to the homomorphism of $G$ to a certain symmetric group $\operatorname{Sym}(V)$,
Also called the group $G$ on the set $V$ action.
One representation is faithful(faithful) If it is injective, only the identity element is mapped to the identity permutation.
The effect of group $G$ on set $V$ also induces other effects,
As it does on the set $V$ power set $2^V$, it gives the permutation between subsets.
Note that the effect preserves the size of the subset, so it can also be applied to the entire subset $k-$ of $V$.
Or change the subset to an ordered tuple.
A subset $S$ of the set $V$ is said to be $G-$ unchanged , if$\,\forall\,s\in S, g\in G,$
$s^g\in S.$ At this time, any $g\in G$ gives the permutation of the elements in $S$,
can be Limit On $S$, it is recorded as $g|_S.$, and the restricted permutation is recorded as $G|_S,$ or $G^S.$.
The function of $G$ on $V$ is transitive , if $x,y\in V,$ is given arbitrarily
There exists $g\in G$ such that $x^g=y.$
$G-$ The invariant subset $S$ is called orbit If $G|_S$ is transitive on $S$.
$\,\forall\,x\in V,$ $x^G:=\{x^g:g\in G\}$ is a orbit.
The orbits do not intersect each other, giving a partition of $V$. Each element falls in exactly one orbit.
Each $G-$ invariant subset is the union of a series of orbits, so the orbits can also be called minimal $G-$ invariant subsets.
count
Let $G$ be the permutation group of $V$, $\,\forall\,x\in V,$
stabilizer $G_x$ is the total permutation of $x^g=x$, forming a subgroup.
Given$S=\{x_1,\cdots,x_r\}\subset V,$
pointwise stabilizer $G_{x_1,\cdots,x_r}:=\bigcap_{i=1}^r G_{x_i},$
collective stabilizer $G_S$ is a total permutation that only requires $S^g=S$. It is easy to see that the former is a subgroup of the latter.
Lemma 1.1. Suppose $G$ acts on $V$, and $S$ is the orbit of $G$. If $x,y\in S,$, then all permutations from $x$ to $y$ will be mapped to a certain right coset of $G_x$. Conversely, all permutations in the right coset of $G_x$ will map $x$ to the same point in $S$.
The proofs in this section are basically basic exercises in abstract algebra and will be skipped here.
Lemma 1.2 (Orbit Stability Set Theorem). $|G_x||x^G|=|G|.$
Take $h\in G,$ and call the elements of the form $g^{-1}hg$ and $h$ conjugate,
All elements conjugated with $h$ are called $h$ conjugate class.
The mapping $\tau_g:h\rightarrow g^{-1}hg$ gives the permutation of $G$,
Therefore $G$ has a conjugation effect on itself, with the conjugate class as the orbit. If $H$ is a subgroup of $G$,
Then $g^{-1}Hg$ is also a subgroup, which is said to be conjugate with $H$.
Lemma 1.3. Suppose $G$ has an effect on $V$, then $\,\forall\,x\in V, g\in G,$ $g^{-1}G_x g=G_{x^g}.$
Let $\operatorname{fix}(g)$ represent the number of fixed points under permutation $g$. We are familiar with the following lemma:
Lemma 1.4 (Burnside). The number of orbits $G$ acts on $V$ is equal to the average number of fixed points of elements in $G$.
asymmetric graph
The picture is asymmetric , if its automorphism group is trivial.
In this section we prove that almost all graphs are asymmetric, that is, for graphs with $n$ points,
The proportion of asymmetric graphs approaches $1.$ when $n\rightarrow \infty$
Assume $V$ contains $n$ points, let $K_V$ be the complete graph of $n$ points.
All graphs containing $n$ points are obtained by deleting edges from $K_V$, so there are a total of $2^{\binom{n}{2} }$ graphs.
Corresponds one-to-one with the $E(K_V)$ subset.
Given a graph $X,$, all graphs isomorphic to it are called $X$ Isomorphism class.Recall the definition of isomorphism,
It can be seen that the isomorphism class is the orbit of the symmetric group $\operatorname{Sym}(V)$ acting on the power set $E(K_V)$.
According to the orbit-stabilizer theorem, there is the following lemma:
Lemma 1.5. The size of the isomorphism class containing $X$ is $\frac{n!}{|\operatorname{Aut}(X)|}.$
By Burnside's lemma, we count isomorphism classes.
Setting $g$ (the generated subgroup) acts on $E(K_V)$ and there are $r$ orbits,
Marked as $\operatorname{orb}_2(g)=r.$, then when $g$ acts on the $E(K_V)$ power set,
These orbits are all minimal $g-$ fixed points, and combined there are a total of $2^r$ fixed points.
Therefore, the number of isomorphism classes of the graph totals $\frac{1}{n!}\sum_{g\in \operatorname{Sym}(V)}2^{\operatorname{orb}_2(g)}$.
If all graphs are asymmetric, then each equivalence class contains $n!$ graphs,
Therefore there are $\frac{2^{\binom{n}{2} } }{n!}$ equivalence classes.
Next we explain that in fact when $n\rightarrow \infty$, the number of equivalence classes tends to this value,
It is further inferred that almost all graphs are asymmetric.
Lemma 1.6. A graph with $n$ vertices has at most $(1+o(1))\frac{2^{\binom{n}{2} } }{n!}$ isomorphism classes.
Certificate: All points that cannot be fixed by a certain permutation are called displaced support,
That is, the effect of permutation is only reflected on the support. It is asserted that for all permutations with support size $2r$,
The $\operatorname{orb}_2$ maximum is achieved by a permutation consisting of $r$ permutations.
The non-permuted fixed point of edge $xy$ is if and only if $x,y$ are both in the support and not in the same permutation,
Or one is in the support and the other is not. The set exchange contains $k$ exchanges,
Then there are $\binom{n-2r}{2}+k$ fixed edges, and each edge is a separate orbit.
For the moving edge, directly consider the number of orbits: one is in the support,
The number of orbits contributed by the edge where the other is not present is at most $(n-2r)(k+2(r-k)/3)=(n-2r)(2r+k)/3$;
The number of orbits that are all in the support and not in the same swap is at most $2k\cdot 2(r-k)/3+k(k-1)+\binom{2(r-k)}{2}/3=4/3 \cdot k(r-k)+k(k-1)+(r-k)(2r-2k-1)/3=[2r^2+k^2-r-2k]/3.$
Together with the previous one, there are at most $\binom{n-2r}{2}+[r(2n-2r-1)+k(k+n-2r+1)]/3$ items in total.
reaches maximum value $(n-2r)(n-2r-1)/2+nr-r^2=n^2/2-rn+r^2-n/2+r=\binom{n}{2}+r(r-n+1).$ at $k=r$
And for a permutation consisting of $k=r$ substitutions,
The previous orbit number only estimates the scale of the $r-k$ part (non-swap part), so when $k=r$,
The calculation is precise,
Therefore the $\operatorname{orb}_2$ maximum is indeed realized by a permutation consisting of $r$ permutations,
And the specific value has been given.
Note that the maximum estimate of the orbit number also holds for permutations with non-even support sizes,
That is, replace $2r$ with the support size $t\in[2,n]$ (the maximum estimate may not be realized at this time).
Then the maximum estimate of the number of orbits $\varphi(t)=\binom{n}{2}+\frac{t}{2}(\frac{t}{2}-n+1)$ is a quadratic function,
Take $t=n-1$ as the axis of symmetry.
Take $m\le n-2,$ and now divide $\operatorname{Sym}(V)$ into three categories: identity transformation,
Supports permutations and remaining permutations whose size does not exceed $m$.
Their sizes respectively do not exceed $1,\binom{n}{m}m!<n^m, n!<n^n.$, estimated by the maximum number of orbits,
Each second type of permutation orbit has at most $\binom{n}{2}-(n-2)$,
Each third type of permutation orbit has at most $\binom{n}{2}-\frac{m}{2}(n-\frac{m}{2}-1)\le \binom{n}{2}-\frac{nm}{4}$.
Therefore, the number of isomorphism classes of the graph is at most $\frac{1}{n!}[2^{\binom{n}{2} }+n^m2^{\binom{n}{2}-(n-2)}+n^n2^{\binom{n}{2}-\frac{nm}{4} }]=\frac{2^{\binom{n}{2} } }{n!}(1+n^m2^{-(n-2)}+n^n2^{-\frac{nm}{4} }).$
Note$n^m2^{-(n-2)}+n^n2^{-\frac{nm}{4} }=2^{m\log_2 n-(n-2)}+2^{n\log_2 n-\frac{nm}{4} },$
It is found that if $m=\lceil 8log_2 n\rceil$ is taken for a sufficiently large $n,$, then this term is an infinitesimal quantity.
Therefore, the number of isomorphism classes is at most $(1+o(1))\frac{2^{\binom{n}{2} } }{n!}$.
Corollary 1.7. Almost all graphs are asymmetric.
Certificate: Assume that among all isomorphism classes, the proportion of isomorphism classes of asymmetric graphs is $\mu.$
Each asymmetric graph contains $n!$ graphs in the isomorphism class,
The other isomorphism classes contain at most $\frac{n!}{2}$ pictures.
Therefore the average size of isomorphism classes is at most $\mu n!+(1-\mu) \frac{n!}{2}=(1+\mu) \frac{n!}{2}.$
And of course every graph appears in a certain isomorphism class,
Therefore $(1+\mu)\frac{n!}{2}(1+o(1))\frac{2^{\binom{n}{2} } }{n!}\ge 2^{\binom{n}{2} },$
$(1+\mu)(1+o(1))\ge 2.$ So when $n\rightarrow\infty$,
$\mu\rightarrow 1.$
Therefore, if all isomorphic graphs are regarded as the same graph, almost all graphs are asymmetric.
If each graph in the isomorphism class is regarded as a different graph, since the asymmetric graph contains the largest number of graphs in the isomorphism class,
We still get that almost all graphs are asymmetric.
the right orbit
Assume $G$ has a transitive effect on $V$, and it will naturally have an effect on $V\times V$,
We study the orbits on it. Since $G$ is transportable and $\{(x,x):x\in V\}$ is an orbit,
called diagonal orbit. Let $\Omega\subset V\times V,$
remember it Transpose $\Omega^T$ is $\{(y,x):(x,y)\in \Omega\}.$
It is easy to see that $\Omega^T$ is invariant to $G-$ if and only if $\Omega$ is also invariant. If $\Omega$ is an orbit,
Then $\Omega=\Omega^T$ or no communication. When $\Omega=\Omega^T$ is called Symmetry Orbit.
Lemma 1.8. Suppose $G$ has a transitive effect on $V$, $x\in V,$, then the orbit of $G$ on $V\times V$ corresponds one-to-one with the orbit of $G_x$ on $V$.
The proof is an exercise in abstraction and will be skipped here.
Therefore, the orbit $\Omega$ of $G$ on $V\times V$ is connected with the orbit of $G_x$ on $V$.
The number of orbits of $G_x$ on $V$ is called the rank of $G$. If $\Omega$ is symmetrical,
It is said that the corresponding orbit of $G_x$ on $V$ is self-paired of.
The orbit $\Omega$ on each $V\times V$ can be viewed as having $V$ as the vertex set,
$\Omega$ is a directed graph of arc sets, and when $\Omega$ is symmetric, it is an undirected graph.
Note that when $\Omega$ is asymmetric, there is only one arc between the two points, which is called oriented
graph).
Lemma 1.9. Let $G$ be the transitive permutation group on $V$, and $\Omega$ be the upper orbit of $V\times V$. Let $(x,y)\in \Omega,$ be the upper orbit of $\Omega$ if and only if $\,\exists\,g\in G,$ makes $(x^g,y^g)=(y,x).$
If $g$ exchanges $x,y,$, then $(xy)$ is exchanged in $g$, then $g$ is of even order, and therefore $G$ is also of even order.
Weigh $G$ on $V$ Generously transitive, if $x,y\in V,$ is given arbitrarily
There is a permutation that exchanges them. All orbits on $V\times V$ are symmetric if and only if $G$ is generously transitive.
Each orbit on $V\times V$ gives a graph, and the elements in $G$ are automorphisms of the graph,
And the effect is transitive on both vertex sets and edge sets. For the union of several orbits,
The elements in $G$ are also automorphisms of the graph, but they only act on the vertex set and are transitive.
Note that $G$ is not necessarily the automorphism group of the graph. The book gives $G=S_7,$ to generate $J(7,3,1),$
However, the example of $S_8\subset \operatorname{Aut}(J(7,3,1))$ is omitted here.
primitivity
Let $G$ be movable on $V$, and the non-empty subset $S\subset V$ is called $G$ Non-original block (block of
imprimitivity), if$\,\forall\,g\in G,$
$S^g=S$ or $S^g\cap S=\varnothing.$ Since $G$ can be migrated,
All transformations of $S$ constitute the division of $V$.
The set of these different transformations is called $G$ system of imprimitivity.
As shown in the figure below, the automorphism group of the cube $Q$ is transitive on the vertex set. It is easy to see when considering the distance.
The set of all points of the same color is a non-primitive block,
The four sets constitute a non-primitive system of automorphism groups.
Except for the case where $S$ is a single point and a universal set, all other non-primitive systems are called non-trivial.
If a group has no non-trivial non-primitive systems, then the group is said to be primitive of,
Otherwise it is non-primitive.
Lemma 1.10. $G$ can transfer to $V$, $x\in V.$ $G$ is primitive if and only if $G_x$ is the maximum subgroup of $G$.
Certificate: Let us prove that $G$ has a non-trivial non-primitive system if and only if $G_x$ is not a maximal subgroup of $G$.
Suppose $G$ has a non-trivial non-primitive system, let $x\in B,$ $B$ be a non-primitive block.
Prove below that $G_x\subsetneq G_B\subsetneq G.$ is due to $\,\forall\,g\in G_x,$
$x\in B\cap B^g,$ Therefore $B=B^g,$ $g\in G_B.$ takes another element $y\neq x.$ in $B$
Due to the existence of mobility $h\in G$, $y=x^h.$ thus $y\in B\cap B^h,$ $B=B^h,$
$h\in G_B.$ However $h\notin G_x,$ therefore $G_x$ is really included in $G_B.$
Let $G_x\subsetneq H\subsetneq G,$
We explain that the orbit of $H$ is the non-trivial non-primitive system of $G$. Let $B$ be the orbit of $H$ containing $x$,
Taking $g\in G,$ requires proof that either $B=B^g,$ or $B\cap B^g=\varnothing.$
Assume $y\in B\cap B^g,$ Since $x,y$ is in the same orbit $B$, $\,\exists\,h\in H,$
So that $y=x^h.$ and since $y\in B^g,$ have elements $x^{h'},$ $x^{h'g}=y.$ in $B$
Therefore $x^{h'gh^{-1} }=x,$ $h'gh^{-1}\in G_x\subsetneq H,$ Therefore $g\in H.$
Since $B$ is the orbit of $H$, there is $B=B^g.$
Since $G_x\subsetneq H,$ $B$ is not only composed of $x$. In order to illustrate that the orbit of $H$ is not the entire $V,$
Recall that $\,\forall\,y\in V,$ $G$ replaces all mappings from $x$ to $y$ to a certain right coset of $G_x$.
If $H$ is also transitive, then $G_x H\supset G.$ has $G_x H=H$, so $H=G,$
It is contradictory to $H$ as a proper subgroup. Therefore $B\neq V$, that is, $B$ is a non-trivial non-primitive system.
Originality and connectivity
Another description of originality is reflected in the orbit of $G$ acting on $V\times V$.
Let's do some preparatory work first.
A path of a directed graph refers to a sequence composed of different vertices $\{u_0,\cdots,u_r\},$
$(u_{i-1},u_i)$ is an arc; a directed graph weak
path) It only requires that $(u_{i-1},u_i)$ or $(u_{i},u_{i-1})$ be an arc.
The directed graph is Strong connectivity , if any two points are connected by a path;
call it weak connectivity This means that any two points are connected by a weak path.
The weak connectivity of a directed graph is the connectivity of an undirected graph regardless of direction. Strongly connected component,
Refers to a strongly connected maximal induced subgraph. According to the definition, a single point is strongly connected,
Therefore a strongly connected component constitutes a partition of the graph.
Vertices in directed graphs in-valency is the number of arcs ending at this point;
out-valency That is the number of arcs starting from this point.
Lemma 1.11. If $D$ is a directed graph with the same out-degree and in-degree of all points, then $D$ is strongly connected if and only if it is weakly connected.
Certificate: Just prove that when $D$ is weakly connected, it is also strongly connected. Otherwise,
$D$ can be split into a strongly connected component $D_1,\cdots,D_r.$ if there is an arc starting from $D_i$ to $D_j,$
Then all arcs connecting $D_i,D_j$ must start from $D_i$,
Otherwise $D_i,D_j$ can be merged into strongly connected subgraphs.
Construct a directed graph $D',$ with the strongly connected components of $D$ as vertices.
There are directed edges from $D_i$ to $D_j$ if and only if there is an arc in $D$ starting from $D_i$ to $D_j.$
Since $D$ is weakly connected, so is $D'$. No cycle can appear in $D'$,
Otherwise, the union of all strongly connected components involved in the ring is strongly connected.
Therefore, it is easy to prove that at least one point in $D'$ has an in-degree of zero, and we might as well assume that it corresponds to a strongly connected component $D_1.$
For all arcs involving $D_1$, if its end point is within $D_1$, the starting point must be within $D_1$,
Out-degree and in-degree cancel; but there is at least one edge starting from $D_1$ and ending outside $D_1$.
Because $D'$ is weakly connected. Therefore, the sum of the out-degrees of all points in $D_1$ must be greater than the in-degree, which is inconsistent with the condition.
Recall that when $G$ can be transferred to $V$, the orbit $\Omega$ on $V\times V$ can be regarded as a directed graph.
When $\Omega$ is asymmetric, the picture is a directed graph. Since $G$ is transitive, all points have the same degree.
The in-degrees are the same. And since the sum of out-degrees is equal to the sum of in-degrees (equal to the number of arcs), the out-degrees of all points are equal to the in-degrees.
Therefore, the strong connectivity of the directed graph corresponding to the orbit is equal to the weak connectivity, which is generally called the connectivity of the orbit.
Lemma 1.12. $G$ is transitive on $V$. $G$ is primitive if and only if every off-diagonal orbit is connected.
Certificate: Assume that $G$ is non-primitive and $B_1,\cdots, B_r$ is a non-primitive system.
Let $x\neq y\in B_1,$ $\Omega$ be the orbit containing $(x,y)$ on $V\times V$. For $g\in G,$
$x^g,y^g$ is in the same non-original block. Therefore, the starting and end points of each arc of $\Omega$ are in the same block,
Obviously not connected.
On the contrary, suppose $\Omega$ is a certain orbit that is not connected, and $B$ is all the vertices of a certain connected component of $\Omega$.
At this time $\,\forall\,g\in G,$ $B^g$ is obviously connected,
Therefore $B^g=B$ or $B^g\cap B=\varnothing.$ therefore $B$ is a non-original block,
$G$ is non-primitive.
The article was last updated on 2021-09-16 14:51:49
