《黎曼几何初步》笔记(3)-测地线

指数映射

测地线

回忆$\gamma:[0,1]\rightarrow M$为测地线的充要条件是$D_{\dot\gamma}\dot\gamma=0.$ 因此若$\gamma$为测地线, 对内积求导可知$|\dot\gamma|$为常数. 因此通过参数变换, 不妨总假定其具单位切向量, 是弧长参数化的. 称其为正规的测地线.

定义

接下来我们引入指数映射的概念. 粗略地说, $x\in M$处的指数映射$\exp:M_x\rightarrow M$定义如下: 任给$v\in M_x,$ 从$x$出发,沿以$v$为初始切向量的测地线$\gamma_v$走到$y,$ 使得$x$到$y$弧长恰为$|v|.$ 那么由$\exp_xv=y$来定义指数映射. 直观看来, $M_x$原点邻域上是可以定义的, 但未必能定义在整体上. 后面将说明指数映射能整体定义等价于要求黎曼流形$M$是完备的.

上述直观在几何上的证明相当笨拙, 用微分方程的方式说明更为简便. 回忆测地线由常微分方程组确定:

$$ \frac{d {}^2\gamma^i}{d {}t^2}+\Gamma^i_{jk}\frac{d {}\gamma^j}{d {}t}\frac{d {}\gamma^k}{d {}t}=0,\quad \,\forall\,i=1,\cdots,n. $$

由ODE基本定理, $\,\forall\,x\in M,$ $\varepsilon>0,$ $\,\exists\,x$的邻域$\mathscr{U}\subset M$以及$\delta>0,$ 使得$\,\forall\,y\in \mathscr{U},$ $v\in B_y(\delta)\subset M_y,$ 存在初始切向量为$v$的测地线$\gamma_v,$ 定义域包含$[0,\varepsilon].$

注意到参数线性变换后的测地线仍是测地线, 因此得到下述命题:

$\,\forall\,x\in M,$ $\,\exists\,x$的邻域$\mathscr{U}\subset M,$ $\omega>0,$ $\,\forall\,y\in \mathscr{U},$ $v\in B_y(\omega)\subset M_y,$ 存在以$v$为初始切向量的测地线$\gamma_v,$ 定义域包含$I=[0,1].$

此时由$\exp_x v=\gamma_v(1)$定义的$\exp_x:B_x(\omega)\rightarrow M$就是满足前述定义的指数映射. 同时, 它可定义在切丛$TM$中的开集$U:=\mathscr{U}\times B(\omega)$上, 由$\exp(y,v):=\exp_y v$给出$\exp:U\rightarrow M.$ 由解对参数的依赖性可知指数映射$\exp$是光滑的.

性质

下面我们说明在小邻域上, 指数映射$\exp_x$是一个微分同胚. 由于$M_x\cong \mathbb{R}^n,$ 其上的切空间自然地等于$M_x$本身. 考虑$(d\exp_x)_O:M_x\rightarrow M_x,$ 容易验证其为恒等映射. 这样它是非奇异的, 从而$\exp_x$在原点邻域的确是微分同胚. 容易证明它在大范围上的叙述:

引理 1. $\,\forall\,K\Subset M,$ $\,\exists\,\varepsilon>0,$ $\,\forall\,x\in K,$ $\exp_x$在$B_x(\varepsilon)$上为微分同胚.

接下来讨论测地线的局部最短性质. 下面默认固定$x,$ 将$x$的下标略去. 设$\exp$在$B(\delta)$上为微分同胚. 记$B_\delta:=\exp B(\delta).$ $\,\forall\,v\in B(\delta),$ 称径向线段$c(t):=tv:[0,1]\rightarrow B_\delta$在指数映射$\exp$下的像为$B_\delta$中的径向测地线. 我们将证明下述定理:

定理 2. 设分段$C^\infty$曲线$\sigma$连接$x,y\in B_\delta.$ 若$\xi$为连接$x,y$的径向测地线, 则$L(\sigma)\ge L(\xi),$ 等号成立当且仅当$\sigma$为$\xi$的单调再参数化.

我们注意到在欧氏空间中这是显然的, 证明只需将曲线的切向量分解为径向分量和球面切向分量即可. 显然没有球面切向时是最短的, 且需要径向分量保持正向. 为了将证明搬到流形上, 需要考虑如何取球面以及做分解.

在$M_x\setminus\{0\}$中定义向量场$\mathscr{R}:$

$$ \mathscr{R}(v)=\frac{v}{|v|},\quad v\in M_x\setminus\{0\}. $$

引理 3. $|d\exp(\mathscr{R})|\equiv 1$

证: $\,\forall\,v\in M_x\setminus\{0\},$ 取$\gamma$为$M$中正规测地线, 以$\frac{v}{|v|}$为初始切向量. 那么$\exp(v)=\gamma(|v|),$

$$ |d\exp(\mathscr{R}(v))|=|\dot{\gamma}(|v|)|=|\dot{\gamma}(0)|=1. $$

引理 4 (Gauss引理). $\,\forall\,t<\delta,$ 令$S_t:=\exp(S(t))$为$B_\delta$中半径为$t$的测地球面, 则径向测地线正交于每一个$S_t.$ 即$d\exp(\mathscr{R})$垂直于$S_t$的切空间.

证: 由于$\exp$是微分同胚, 可以取到如下微分同胚:

$$ F:S^{n-1}\times(0,\delta)\rightarrow B_\delta\setminus\{x\}, $$

其中$S^{n-1}=S(1)$为$M_x$中单位球面. $F(p,t):=\exp(tp).$ 对每个固定的$t,$ $F$将$S^{n-1}\times\{t\}$微分同胚地映至$S_t.$ 取$S^{n-1}$局部坐标系$\{y^i\},$ $r$为$(0,\delta)$上的自然参数, 记$R=dF\left(\frac{\partial {} }{\partial {}r}\right),$ $Y_i=dF\left(\frac{\partial {} }{\partial {}r}\right),$ 则只需证$\left<{}Y_i,R\right>=0.$

$$ \begin{aligned} R\left<{}Y_i,R\right>&=\left<{}D_RY_i,R\right>+\left<{}Y_i,D_RR\right>\\ &=\left<{}D_{Y_i}R,R\right>&D_RY_i-D_{Y_i}R=[R,Y_i]=dF\left[\frac{\partial {} }{\partial {}r},\frac{\partial {} }{\partial {}y_i}\right], D_RR=0\\ &=\frac{1}{2}Y_i\left<{}R,R\right>=0&|R|\equiv 1 \end{aligned} $$

因此$\left<{}Y_i,R\right>$沿径向测地线为常数. 由于当$z\rightarrow x$时, $Y_i(z)\rightarrow 0,$ $\left<{}Y_i,R\right>\rightarrow 0.$ 因此 $\left<{}Y_i,R\right>\equiv 0.$

有了这两个引理, 就可以仿照欧氏空间, 将定理的证明搬运到流形上了. 只需将曲线的切向量分解为$d\exp(\mathscr{R})$与$S_t$切空间上的分量, 求长度, 说明只具$d\exp(\mathscr{R})$上分量且保持正向时, 曲线最短即可. 特别地, 此时曲线即为径向测地线的单调再参数化.

由该定理可知, 最短线一定是测地线, 不然局部上可以取测地线将曲线改造得更短. 但反过来不一定成立, 测地线不见得是最短的, 如考虑球面与圆柱面上的测地线.

度量完备性

事实上, 流形上并不见得存在最短线, 如圆盘挖去中心点. 这就牵涉到流形完备性的讨论. 我们现在在$M$上引入距离空间结构, 通常也叫度量空间结构.

定义$d(x,y)=\inf_{\gamma}L(\gamma),$ $\gamma$为连接$x,y$的$C^\infty$曲线. 断言$d$是$M$上的距离. 只需证明$x\neq y$时, $d(x,y)\neq 0.$ 这并不是显然的, 因为定义里涉及到了下确界. 不过由前面的测地线局部最短性质, 下确界局部上是可以达到的. 因此接下来只要说明$y\not\in B_\delta,$ $d(x,y)\ge \delta>0$即可, 而这是容易说明的.

由于度量$g_{ij}$是连续变换的, 它的最小最大特征值也是, 从而紧集上有$\varepsilon|v|^2\le g_{ij}v^iv^j\le \alpha|v|^2.$ 这能够说明距离空间$(M,d)$与原先流形上的拓扑是一致的. 称黎曼流形$M$是完备的, 若$(M,d)$是一个完备的距离空间.

定理 5 (Hopf-Rinow定理). 在一个黎曼流形中, 下述条件是等价的:

$M$是完备的.
$\,\forall\,x\in M,$ $\exp_x$定义在整个$M_x$上.
$\,\exists\,x\in M,$ $\exp_x$定义在整个$M_x$上.
$M$中每个有界闭集是紧的.

证: 我们来证明$(1)\Rightarrow(2)\Rightarrow (3)\Rightarrow (4)\Rightarrow (1),$ 不过只有$(1)\Rightarrow (2),$ $(3)\Rightarrow (4)$不是那么平凡的.

对于$(1)\Rightarrow (2),$ 只需说明每条正规测地线能无限延伸. 倘若测地线只能延伸到$(a,b),$ 那么由完备性, $x=\lim\limits_{t\rightarrow b}\gamma(t)\in M.$ 那么在$x$点附近就可以延伸测地线了.

$(3)\Rightarrow (4)$是较为困难的. 首先考虑已有的$\exp_x:M_x\rightarrow M.$ 记$\overline{B}_r:=\exp_x\overline{B(r)},$ 那么紧集的连续像也是紧的. 对任意有界闭集$K,$ 只需证明$\,\exists\,\overline{B}_r\supset K,$ 这样紧集中闭集也是紧的. 为此我们证明如下命题: $\,\forall\,y\in M,$ 存在最短测地线连接$x,y.$ 这样有界集便总能被某个测地球包含.

$\,\forall\,y\in M,$ 设$d(x,y)=r.$ 取$\delta>0$使得$\overline{B}_{\delta}$上指数映射是微分同胚. 取$x_\delta\in S_\delta=\partial B_\delta,$ 使得$d(x_\delta,y)$达到最小. 那么$x_\delta=\exp{\delta v},$ $|v|=1.$ 断言由$v$引出的测地线$\gamma(t)=\exp(tv)$满足$\gamma(r)=y.$ 这样测地线$\gamma$即是连接$x,y$的最短曲线, 命题得证.

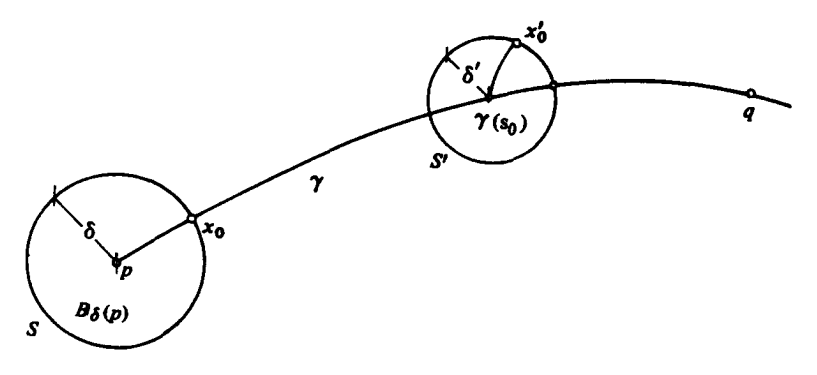
我们采用连续性方法证明. 记$A:=\{s\in[0,r]:d(\gamma(s),y)=r-s\}.$ 首先$0\in A,$ $A$非空. 其次由连续性$A$当然是闭的. 只需证明$A$是开的, 即有$A=[0,r].$ 这样就推得了$\gamma(r)=y.$

$\,\forall\,s\in A,$ 考虑$\gamma(s)$处的$\overline{B}_{\delta'},$ 使得指数映射在其上为微分同胚. 取$x_{\delta'}\in S_{\delta'}$使得$d(x_{\delta'},y)$达到最小. 欲证$d(\gamma(s+\delta'),y)=r-s-\delta'.$ 已知

$$ d(\gamma(s),x_{\delta'})=\delta', \quad d(\gamma(s),y)=r-s=\delta'+\min_{x'\in S_{\delta'} }d(x',y), $$

因此$d(x_{\delta'},y)=r-s-\delta',$ 只需说明$\gamma(s+\delta')=x_{\delta'}.$ 注意到

$$ d(x,x_{\delta'})\ge d(x,y)-d(x_{\delta'},y)=s+\delta', $$

而连接$x\sim\gamma(s),$ $\gamma(s)\sim x_{\delta'}$的两段测地线拼接起来刚好弧长为$s+\delta'.$ 回忆最短线一定是测地线, 因此这个分段曲线是测地线. 由测地线的分析性质, 曲线实际上是整体不分段的, 故连接$\gamma(s)\sim x_{\delta'}$的部分就是$\gamma(s)$处测地线的延伸, 从而$\gamma(s+\delta')=x_{\delta'}.$ 至此论证完毕.

在证明过程中, 我们看到了如下推论:

推论 6. 在一个完备的黎曼流形中, 任意两点均可用一条最短测地线连接.

推论 7. 在一个完备的黎曼流形$M$中, $\exp_x:M_x\rightarrow M$是满的, $\,\forall\,x\in M.$

文章最后更新于 2022-03-13 18:52:14

exponential mapping

geodesic

Memories$\gamma:[0,1]\rightarrow M$ are geodesic The necessary and sufficient condition is $D_{\dot\gamma}\dot\gamma=0.$ Therefore, if $\gamma$ is a geodesic, derivation of the inner product shows that $|\dot\gamma|$ is a constant. Therefore, through parameter transformation, we may always assume that it has a unit tangent vector and is parameterized by arc length. call it unit-speed Geodesics.

definition

Next we introduce exponential mapping concept. Roughly speaking, The exponential mapping $\exp:M_x\rightarrow M$ at $x\in M$ is defined as follows: given $v\in M_x,$ Start from $x$ and walk along the geodesic $\gamma_v$ with $v$ as the initial tangent vector to $y,$ So that the arc length from $x$ to $y$ is exactly $|v|.$, then the exponential mapping is defined by $\exp_xv=y$. Intuitively, $M_x$ It can be defined in the neighborhood of the origin, but it may not be defined as a whole. It will be explained later that the overall definition of exponential mapping is equivalent to requiring that the Riemannian manifold $M$ is complete.

The geometric proof of the above intuition is quite clumsy, and it is simpler to explain it in the form of differential equations. Recall that geodesics are determined by a system of ordinary differential equations:

$$ \frac{d {}^2\gamma^i}{d {}t^2}+\Gamma^i_{jk}\frac{d {}\gamma^j}{d {}t}\frac{d {}\gamma^k}{d {}t}=0,\quad \,\forall\,i=1,\cdots,n. $$

According to the basic theorem of ODE, $\,\forall\,x\in M,$ $\varepsilon>0,$ Neighborhoods $\mathscr{U}\subset M$ and $\delta>0,$ of $\,\exists\,x$ Make$\,\forall\,y\in \mathscr{U},$ $v\in B_y(\delta)\subset M_y,$ There is a geodesic $\gamma_v,$ with initial tangent vector $v$ whose domain contains $[0,\varepsilon].$

Note that the geodesic after linear transformation of parameters is still a geodesic, so the following proposition is obtained:

$\,\forall\,x\in M,$ Neighborhood $\mathscr{U}\subset M,$ of $\,\exists\,x$ $\omega>0,$ $\,\forall\,y\in \mathscr{U},$ $v\in B_y(\omega)\subset M_y,$ There is a geodesic $\gamma_v,$ with $v$ as the initial tangent vector. The domain contains $I=[0,1].$

At this time, $\exp_x:B_x(\omega)\rightarrow M$ defined by $\exp_x v=\gamma_v(1)$ is an exponential mapping that satisfies the aforementioned definition. At the same time, it can be defined on the open set $U:=\mathscr{U}\times B(\omega)$ in the tangent bundle $TM$, $\exp:U\rightarrow M.$ is given by $\exp(y,v):=\exp_y v$ It can be seen from the dependence of the solution on the parameters that the exponential map $\exp$ is smooth.

nature

Below we explain that in small neighborhoods, the exponential map $\exp_x$ is a diffeomorphism. Since $M_x\cong \mathbb{R}^n,$ the tangent space above it is naturally equal to $M_x$ itself. Considering $(d\exp_x)_O:M_x\rightarrow M_x,$, it is easy to verify that it is an identity mapping. In this way, it is non-singular, so $\exp_x$ is indeed diffeomorphism in the neighborhood of the origin. It is easy to prove its statement on a large scale:

Lemma 1. $\,\forall\,K\Subset M,$ $\,\exists\,\varepsilon>0,$ $\,\forall\,x\in K,$ $\exp_x$ is diffeomorphism on $B_x(\varepsilon)$.

Next, we discuss the local shortest property of the geodesic. In the following, $x,$ is fixed by default and the subscript of $x$ is omitted. Let $\exp$ be diffeomorphism on $B(\delta)$. Let $B_\delta:=\exp B(\delta).$ $\,\forall\,v\in B(\delta),$ weigh Radial segment The image of $c(t):=tv:[0,1]\rightarrow B_\delta$ under exponential mapping $\exp$ is in $B_\delta$ Radial geodesics. We will prove the following theorem:

Theorem 2. Suppose the piecewise $C^\infty$ curve $\sigma$ connects $x,y\in B_\delta.$. If $\xi$ is a radial geodesic connecting $x,y$, then $L(\sigma)\ge L(\xi),$ is equal if and only if $\sigma$ is a monotonic reparameterization of $\xi$.

We note that this is obvious in Euclidean space, It is proved that it is only necessary to decompose the tangent vector of the curve into a radial component and a spherical tangential component. Obviously it is the shortest when there is no spherical tangent, and the radial component needs to be kept positive. In order to move the proof to a manifold, we need to consider how to take the sphere and decompose it.

Define vector field $\mathscr{R}:$ in $M_x\setminus\{0\}$

$$ \mathscr{R}(v)=\frac{v}{|v|},\quad v\in M_x\setminus\{0\}. $$

Lemma 3. $|d\exp(\mathscr{R})|\equiv 1$

Certificate: $\,\forall\,v\in M_x\setminus\{0\},$ Take $\gamma$ as the unit-speed geodesic in $M$, and $\frac{v}{|v|}$ as the initial tangent vector. Then $\exp(v)=\gamma(|v|),$

$$ |d\exp(\mathscr{R}(v))|=|\dot{\gamma}(|v|)|=|\dot{\gamma}(0)|=1. $$

Lemma 4 (Gauss’ lemma). $\,\forall\,t<\delta,$ Let $S_t:=\exp(S(t))$ be the geodesic surface with radius $t$ in $B_\delta$, then the radial geodesic is orthogonal to each $S_t.$, that is, $d\exp(\mathscr{R})$ is perpendicular to the tangent space of $S_t$.

Certificate: Since $\exp$ is a diffeomorphism, the following diffeomorphism can be obtained:

$$ F:S^{n-1}\times(0,\delta)\rightarrow B_\delta\setminus\{x\}, $$

Where $S^{n-1}=S(1)$ is the unit sphere in $M_x$. $F(p,t):=\exp(tp).$ For each fixed $t,$ $F$, diffeomorphically map $S^{n-1}\times\{t\}$ to $S_t.$ Take $S^{n-1}$ local coordinate system $\{y^i\},$ $r$ as the natural parameters on $(0,\delta)$, Note$R=dF\left(\frac{\partial {} }{\partial {}r}\right),$ $Y_i=dF\left(\frac{\partial {} }{\partial {}r}\right),$ Then you only need to prove $\left<{}Y_i,R\right>=0.$

Therefore $\left<{}Y_i,R\right>$ is constant along the radial geodesic. Since when $z\rightarrow x$, $Y_i(z)\rightarrow 0,$ $\left<{}Y_i,R\right>\rightarrow 0.$ Therefore $\left<{}Y_i,R\right>\equiv 0.$

With these two lemmas, we can imitate the Euclidean space and transfer the proof of the theorem to the manifold. Just decompose the tangent vector of the curve into components on the tangent space $d\exp(\mathscr{R})$ and $S_t$, Find the length and show that when it only has the upper component of $d\exp(\mathscr{R})$ and remains positive, the curve will be the shortest. In particular, the curve at this time is a monotonic reparameterization of the radial geodesic.

It can be seen from this theorem that the shortest line must be a geodesic. Otherwise, the local geodesic can be used to transform the curve into a shorter one. But the converse may not necessarily be true. The geodesic is not necessarily the shortest, for example, consider the geodesics on the sphere and cylinder.

Metric completeness

In fact, there may not necessarily be a shortest line on the manifold, such as a disk digging out the center point. This involves manifolds Completeness discussion. We now introduce on $M$ distance space structure, Usually also called metric space structure.

Definition$d(x,y)=\inf_{\gamma}L(\gamma),$ $\gamma$ is the $C^\infty$ curve connecting $x,y$. Assert that $d$ is the distance on $M$. It is only necessary to prove $x\neq y$ that $d(x,y)\neq 0.$ is not obvious, Because the definition involves the lower bound. However, based on the local shortest property of the geodesic, The indefinite bound is locally achievable. So next we only need to explain $y\not\in B_\delta,$ $d(x,y)\ge \delta>0$ will do, and this is easy to explain.

Since the metric $g_{ij}$ is continuously transformed, its minimum and maximum eigenvalues are also, Therefore, there is $\varepsilon|v|^2\le g_{ij}v^iv^j\le \alpha|v|^2.$ on the compact set This can show that the distance space $(M,d)$ is consistent with the topology on the original manifold. The Riemannian manifold $M$ is said to be complete if $(M,d)$ is a complete distance space.

Theorem 5 (Hopf-Rinow theorem). In a Riemannian manifold, the following conditions are equivalent:

$M$ is complete.
$\,\forall\,x\in M,$ $\exp_x$ defined throughout $M_x$ on.
$\,\exists\,x\in M,$ $\exp_x$ defined throughout $M_x$ on.
$M$ Every bounded closed set in is compact.

Certificate: Let’s prove $(1)\Rightarrow(2)\Rightarrow (3)\Rightarrow (4)\Rightarrow (1),$ But only $(1)\Rightarrow (2),$ $(3)\Rightarrow (4)$ are not so trivial.

For $(1)\Rightarrow (2),$, it only needs to be stated that each unit-speed geodesic can extend infinitely. If the geodesic can only extend to $(a,b),$ then by completeness, $x=\lim\limits_{t\rightarrow b}\gamma(t)\in M.$ Then the geodesic can be extended near the $x$ point.

$(3)\Rightarrow (4)$ is more difficult. Consider existing ones first $\exp_x:M_x\rightarrow M.$ Note $\overline{B}_r:=\exp_x\overline{B(r)},$ then the continuous image of the compact set is also compact. For any bounded closed set $K,$ only need to prove $\,\exists\,\overline{B}_r\supset K,$ In this way, the compact set and the closed set are also compact. For this reason, we prove the following proposition: $\,\forall\,y\in M,$ There is a shortest geodesic connection $x,y.$ In this way, the bounded set can always be contained by some geodesic.

$\,\forall\,y\in M,$ Let $d(x,y)=r.$ Take $\delta>0$ so that the exponential map on $\overline{B}_{\delta}$ is a diffeomorphism. Take $x_\delta\in S_\delta=\partial B_\delta,$ to make $d(x_\delta,y)$ minimum. Then $x_\delta=\exp{\delta v},$ $|v|=1.$ Assert that the geodesic $\gamma(t)=\exp(tv)$ derived from $v$ satisfies $\gamma(r)=y.$ In this way, the geodesic $\gamma$ is the shortest curve connecting $x,y$, and the proposition is proved.

We use the continuity method to prove. Note $A:=\{s\in[0,r]:d(\gamma(s),y)=r-s\}.$ First of all, $0\in A,$ $A$ is not empty. Secondly, $A$ is of course closed due to continuity. Just prove that $A$ is open, That is, there is $A=[0,r].$, so we can deduce $\gamma(r)=y.$

$\,\forall\,s\in A,$ Consider $\overline{B}_{\delta'},$ at $\gamma(s)$ Make the exponential map on it a diffeomorphism. Take $x_{\delta'}\in S_{\delta'}$ to make $d(x_{\delta'},y)$ minimum. Want to prove $d(\gamma(s+\delta'),y)=r-s-\delta'.$ Known

$$ d(\gamma(s),x_{\delta'})=\delta', \quad d(\gamma(s),y)=r-s=\delta'+\min_{x'\in S_{\delta'} }d(x',y), $$

Therefore $d(x_{\delta'},y)=r-s-\delta',$ Just state that $\gamma(s+\delta')=x_{\delta'}.$ noticed

$$ d(x,x_{\delta'})\ge d(x,y)-d(x_{\delta'},y)=s+\delta', $$

And connect$x\sim\gamma(s),$ The arc length of the two geodesics of $\gamma(s)\sim x_{\delta'}$ when spliced together is $s+\delta'.$ Recall that the shortest line must be a geodesic, so this piecewise curve is a geodesic. According to the analytical properties of geodesics, The curve is actually not segmented as a whole. Therefore, the part connected to $\gamma(s)\sim x_{\delta'}$ is the extension of the geodesic at $\gamma(s)$, Thus $\gamma(s+\delta')=x_{\delta'}.$ the argument is completed.

During the proof, we saw the following inference:

Corollary 6. In a complete Riemannian manifold, any two points can be connected by a shortest geodesic.

Corollary 7. In a complete Riemannian manifold $M$, $\exp_x:M_x\rightarrow M$ is full, $\,\forall\,x\in M.$

The article was last updated on 2022-03-13 18:52:14