《黎曼几何初步》笔记(4)-等距变换和空间形式

介绍

现在开始我们对空间形式, 即常截面曲率的完备黎曼流形进行研究. 我们有如下基本结果:

定理 1. $\,\forall\,c\in \mathbb{R},$ $n\in \mathbb{Z}_+,$ $\,\exists\,$等距变换下唯一的常截面曲率$c$的单连通$n$维空间形式.

定理完整证明于下章给出, 本节我们注重于存在性部分. 设有黎曼度量$g,$ 截面曲率为$K,$ 那么对于正常数$A,$ 度量$Ag$的截面曲率为$\frac{1}{A}K.$ 因此我们只需考虑截面曲率为$0,\pm 1$的空间形式. 对于$c=0,$ 取$\mathbb{R}^n$即可; 对于$c=1,$ 取熟知的单位球面$S^n$即可; 对于$c=-1,$ 需要取配备双曲度量, 即

$$g=\frac{4}{\left(1-\sum_i \left(x^i\right)^2\right)^2}\sum_i dx^i\otimes dx^i$$

的单位球$B^n.$ 我们引入新的概念后来说明后两个结论.

全测地子流形

定义

设$M$为黎曼流形$\overline{M}$的子流形, 配备诱导度量. 若$\overline{M}$中任一与$M$相切的测地线全部位于$M$中, 则称$M$是$\overline{M}$中的全测地子流形. 可以看出, 全测地子流形是十分稀少的, 几乎所有黎曼流形都没有任何全测地子流形. 不过由此可以引入一个新的几何量, 这是十分有意义的.

引理 2. $M$是$\overline{M}$的全测地子流形的充要条件是, 对$M$中任何向量场$X,Y,$ $D_XY=\overline{D}_XY,$ 这里$D,\overline{D}$分别为$M,\overline{M}$上的Levi-Civita联络.

证: 首先设$M$是$\overline{M}$的任一子流形. 对$M$中向量场$X,Y,$ 定义

$$S(X,Y):=D_XY-\overline{D}_XY,$$

$S(X,Y)$是$\overline{M}$中仅定义在$M$上的向量场. 此时, 对$M$上任意函数$f,$

$$S(fX,Y)=fS(X,Y)=S(X,fY).$$

因此可定义$S:M_x\otimes M_x\rightarrow \overline{M}_x,$

$$S(v,w)=S(V,W),\quad \,\forall\,V(x)=v,W(x)=w\in M_x,$$

$V,W$为$M$中任意满足上述条件的向量场. 由Levi-Civita联络的对称性可知,

$$S(v,w)=S(w,v).$$

现设$M$为$\overline{M}$的全测地子流形, 断言:

$$S(v,v)=0,\quad \,\forall\,v\in M_x, x\in M.$$

设$\gamma$为$\overline{M}$中以$v$为初始切向量的测地线, $\overline{D}_{\dot\gamma}\dot\gamma=0,$ 则$\gamma$也是$M$中测地线, $D_{\dot\gamma}\dot\gamma=0.$ 因此

$$S(v,v)=D_{\dot\gamma(0)}\dot\gamma-\overline{D}_{\dot\gamma(0)}\dot\gamma=0.$$

从而,

$$S(v+w,v+w)=2S(v,w)=0\,\Rightarrow\, D_XY=\overline{D}_XY,\quad \,\forall\,X,Y\in \mathfrak{X}(M).$$

反之, 设$S\equiv 0.$ 取$\overline{M}$中与$M$相切的测地线$\gamma,$ 欲说明$\gamma\subset M.$ 取$M$中测地线$\xi,$ 与$\gamma$初始切向量相同. 此时,

$$\overline{D}_{\dot\xi}\dot\xi=D_{\dot\xi}\dot\xi\equiv 0,$$

因此$\xi$也是$\overline{M}$中测地线. 由唯一性即知$\xi=\gamma,$ 从而$\gamma$确实落在$M$中.

注 3. 上述$S$称为$M$在$\overline{M}$中的第二基本形式, 关于它的讨论将在后续章节提到.

由于曲率张量由Levi-Civita联络定义, 我们有如下推论:

引理 4. 设$M$是$\overline{M}$的一个全测地子流形, $K,\overline{K}$分别为$M,\overline{M}$的截面曲率函数, 则$\,\forall\,x\in M,$ 对于任意$2$-平面$\Pi\subset M_x,$ $K(\Pi)=\overline{K}(\Pi).$

等距变换

我们先看一个例子, 设$\gamma$为弧长参数曲线, 且存在等距变换$\varphi$以$\gamma$为固定点集. 那么断言$\gamma$为正规测地线. $\,\forall\,t,$ 取$\xi$为以$\dot{\gamma}(t)$为初始切向量的测地线, 那么由于等距变换保持局部极短性质, $\varphi(\xi)$也是测地线, 且以$d\varphi (\dot\gamma(t))=\dot\gamma(t)$为初始切向量. 由唯一性知$\varphi(\xi)=\xi,$ $\xi$轨迹为固定点集, 从而$\gamma$与$\xi$在公共定义域上相同, 为正规测地线. 更一般地, 我们有如下结论:

引理 5. 一个等距变换的固定点集为全测地子流形(不一定连通).

证: 只需集中证明$\overline{M}$关于等距变换$\varphi$的固定点集$M$的确是一个子流形, 其后的说明与前面的讨论一致. 定义

$$\mathscr{F}:=\{v\in \overline{M}_x:d\varphi(v)=v\},$$

只需说明$\exp_x(\mathscr{F}\cap B(\delta))=M\cap B_\delta,$ 其中$\delta$充分小使$\exp_x$在球上是微分同胚. 这样就建立了$M$上的坐标邻域, 使之成为子流形. 关于这一点的证明, 同样注意利用等距变换保持测地性, 以及测地线的唯一性即可.

空间形式

单位球面

引理 6. 单位球面$S^n$具常截面曲率$+1,$ $\,\forall\,n\ge 2.$

证: $n=2$时, $S^2$截面曲率即高斯曲率, 熟知为$+1.$ 对$n\ge 3,$ 记$x\in \mathbb{R}^3,$ $y\in \mathbb{R}^{n-2},$ $\mathbb{R}^{n+1}$上的等距变换$\widetilde\varphi:(x,y)=(x,-y)$诱导了$S^n$上的等距变换$\varphi,$ 以$\{(x,0)\}=S^2$为固定点集. 因此$S^2$是一个全测地子流形, 由引理, $S^n$中与该$S^2$相切平面的截面曲率与$S^2$截面曲率相同, 为$+1.$ 而对于$S^n,$ 任意两点处任意两个二维切平面间存在一个等距变换, 因此它是以$+1$为常截面曲率的空间形式.

双曲度量

引理 7. 配备双曲度量的单位球$B^n$是常截面曲率为$-1$的完备黎曼流形.

证: 首先讨论完备性. 由Hopf-Rinow定理, 我们可以证明从原点出发的测地线总可无限延伸, 进而$\exp_O$定义在整个切空间上, 从而流形是完备的. 考虑曲线$\xi(s)=\left(\frac{e^s-1}{e^s+1},0,\cdots,0\right).$ 计算得到$s$为弧长参数, 且$\xi$为等距变换$(x^1,x^2,\cdots,x^n)\mapsto (x^1,-x^2,\cdots,-x^n)$的不动点集, 故$\xi$是测地线. 进而由对称性, 沿各个方向出发的测地线均可无限延伸.

接下来, 取$B^n$在$p$点的任一切平面$\Pi\subset \mathbb{R}^n,$ 取$E$为包含$\Pi,p$的任一$3$维子空间. 由对称性, 不妨假设$E=\mathbb{R}^3,$ 那么$E\cap B^n=B^3$是等距变换$(x^1,x^2,x^3,x^4,\cdots,x^n)\mapsto (x^1,x^2,x^3,-x^4,\cdots,-x^n)$的不动点集, 为全测地子流形. 因此只需证明$B^3$在诱导双曲度量下具常截面曲率$-1$即可. 为此采用球坐标计算即可. $n=2$的情形直接采用极坐标计算即可.

后面我们将配备双曲度量的单位球记作$H^n.$

测地线性质

接下来我们在空间形式中考虑测地线的性质. 直观来看, 考虑从一点出发的固定初始切向量夹角的两条测地线, 若以$\mathbb{R}^n$为基准, $S^n$的相比之下要靠拢, 而$H^n$的要发散. 这是截面曲率与测地线间的重要联系. 接下来我们取$n=2$来严格表述这一点. 注意由于$n=2$的情形为各自一般情形的全测地子流形, 对一般的$n$性质也是成立的.

现设$M=\mathbb{R}^2,S^2,H^2,$ 选定参考点$O\in M,$ 定义半径为$r$的测地圆周:

$$C(r)=\{x\in M,d(0,x)=r\}.$$

当$r$充分小时, $C(r)$即为$M_O$中半径为$r$的圆周在微分同胚$\exp_O$下的像. 它的长度就衡量了$M$上从$O$点出发测地线的散开率.

设$c_0(r),c_+(r),c_-(r)$分别是$\mathbb{R}^2,S^2,H^2$中$C(r)$的长度. 显然$c_0(r)=2\pi r,$ $c_+(r)=2\pi \sin r.$ 最后计算可得$c_-(r)=2\pi \sinh r.$ 它们都是齐性空间($H^n$的齐性将在后面说明), 因此参考点$O$选取不影响$C(r)$长度. 由图像立即可见负曲率将测地线推开, 而正曲率将测地线汇拢.

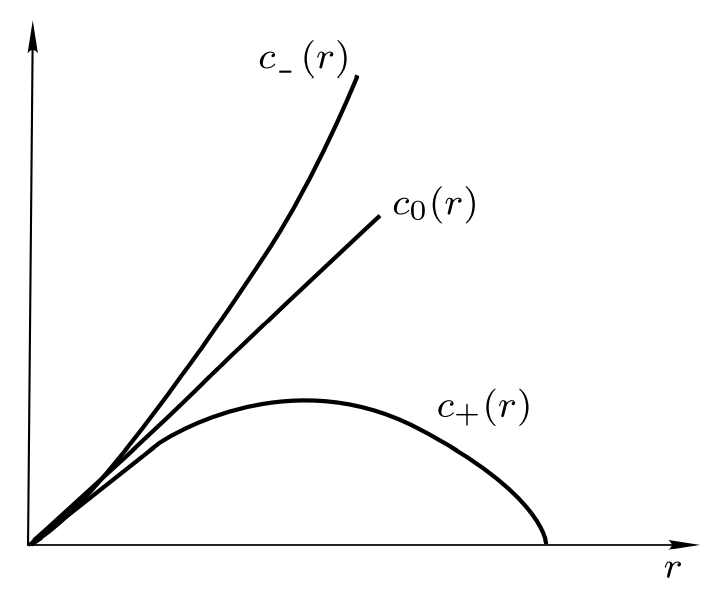
对任意完备二维黎曼流形$M,$ 选定参考点$O\in M,$ 我们也来考虑测地圆周$C(r)$的长度$c(r).$ 令$r$充分小, 则

$$c(r)=\int_0^{2\pi}\left|d\exp_O\left(\frac{d {} }{d {}\theta}(r,\theta)\right)\right|d\theta.$$

可以看出我们不需要特别考虑$d\exp$对径向方向的影响. 我们先转而研究另一个对象, 之后再回来继续讨论这个问题.

Jacobi场

所谓$C^\infty$矩阵映射, 是指光滑映射$\gamma:[a,b]\times [c,d]\rightarrow M.$ 可由此定义两个沿$\gamma$的向量场$T,U:$

$$T(\gamma(t,u)):=d\gamma\left(\frac{\partial {} }{\partial {}t}(t,u)\right),\quad U(\gamma(t,u)):=d\gamma\left(\frac{\partial {} }{\partial {}u}(t,u)\right).$$

每一个$u\in[c,d]$确定了一条曲线$\gamma_u(t)=\gamma(t,u).$ 当$0\in[c,d]$时, 称$\gamma_0$为$C^\infty$矩形$\gamma$的基曲线. 若再假设每一条$\gamma_u$是$M$的测地线, 则称矩阵映射$\gamma$是单参数测地线族$\{\gamma_u\}.$ 于是我们有

$$[T,U]=d\gamma\left(\left[\frac{\partial {} }{\partial {}t},\frac{\partial {} }{\partial {}u}\right]\right)=0,\quad D_TT=0.$$

进而,

$$D_TD_TU=D_TD_UT=D_TD_UT-D_UD_TT-D_{[T,U]}T=-R_{TU}T.$$

限制在基曲线上, 我们就得到了:

$$\ddot{U}+R_{\dot{\gamma}_0U}\dot{\gamma}_0=0.$$

称上式为Jacobi方程, 称沿曲线$\gamma_0,$ 符合上式的向量场$U$为Jacobi场. 称向量场$U$为$\{\gamma_u\}$的横截向量场, 于是得到:

引理 8. 单参数测地线族的横截向量场沿基曲线是一个Jacobi场.

反过来, 后面我们将说明沿测地线的每个Jacobi场都是某个单参数测地线族的横截向量场. 下面我们重新回到原来的讨论. 我们说明$d\exp_O\left(\frac{d {} }{d {}\theta}\right)$是某个单参数测地线族的横截向量场, 从而Jacobi方程就给出了曲率与$d\exp_O\left(\frac{d {} }{d {}\theta}\right)$之间决定性的联系, 也就可以看出曲率和$c(r)$之间的重要关系.

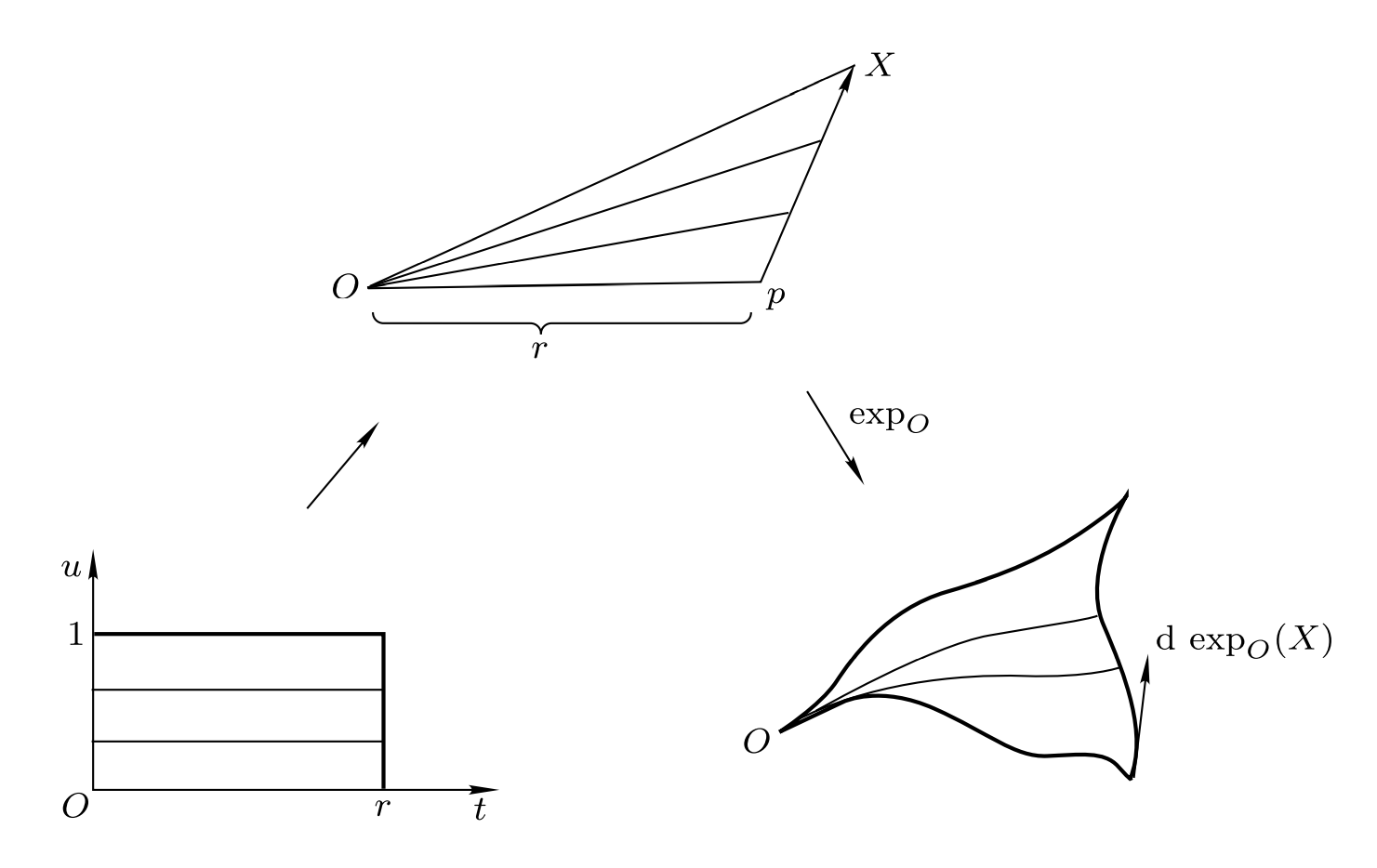
设$p\in M_O,$ $X$为$M_O$中向量, 那么$\Gamma(t,u):=\exp_O\frac{t}{r}(p+uX)$就定义了一个单参数测地线族, $r=|p|,$ 满足

$$U(0)=0,\quad \dot{U}(0)=\frac{1}{r}X.$$

为证明第二个式子, 引入由$\exp_O:B(\delta)\approx B_\delta$决定的坐标系, 称为法坐标系, 满足:

$$\left\{\begin{aligned} &\left<{}\frac{\partial {} }{\partial {}x^i}(0),\frac{\partial {} }{\partial {}x^j}(0)\right>=\delta_{ij},&\,\forall\,i,j,\\ &D_{\frac{\partial {} }{\partial {}x^i}(0)}\frac{\partial {} }{\partial {}x^j}=0,&\,\forall\,i,j. \end{aligned}\right.$$

一式显然. 对于二式, 定义$\beta:M_O\times M_O\rightarrow \mathbb{R},$ $\beta(e_i,e_j)=D_{\frac{\partial {} }{\partial {}x^i}(0)}\frac{\partial {} }{\partial {}x^j},$ 做线性延拓成为一个对称双线性型. 由于法坐标系下径向直线都是测地线, $\beta(v,v)=0,$ 从而$\beta\equiv 0,$ 这就得到了第二式, 因此在法坐标系下, $\Gamma_{ij}^k\equiv 0.$

现在就可以回来说明$\dot{U}(0)=\frac{1}{r}X.$ 由于$X$为常向量, $\Gamma_{ij}^k\equiv 0,$

$$D_{\dot{\gamma}_0(0)}U=\frac{1}{r}X+\frac{t}{r}D_{\dot{\gamma}_0(0)}X=\frac{1}{r}X.$$

现取$X=\frac{d {} }{d {}\theta}(r,\theta)$就说明了$d\exp_O\left(\frac{d {} }{d {}\theta}\right)$确为某个单参数测地线族的横截向量场. 设$\gamma$是基曲线$\Gamma_0,$ $W(t)$为沿$\gamma$的单位平行向量场, $W(t)\perp\dot{\gamma}(t).$ 对于横截向量场$U,$ 由Gauss引理, 它也与$\dot{\gamma}(t)$正交. 因此$U(t)=f(t)W(t).$ 由Jacobi方程,

$$\ddot{f}+Kf=0,\quad f(0)=0,\quad \dot{f}(0)=1. \eqno{(\ast )}$$

这里$K(t)$为$\gamma(t)$处的Gauss曲率.

应用到二维空间形式上, 我们就得到了:

$$f(r)=\left\{\begin{aligned} &r, &&K=0,\\ &\sin r, &&K=+1,\\ &\sinh r, &&K=-1. \end{aligned}\right.$$

这就是先前所求的$c_0,c_+,c_-.$ $(\ast )$式由Jacobi发现, 称其中的初始条件为标准的初始条件.

由于曲率控制测地线的性质, 可以预想到充分正曲率的流形应当是紧的(Bonnet-Myers定理), 而负曲率流形让我们期望一点处的指数映射将是一个微分同胚(Cartan-Hadamard定理).

最后给出一些评注. 假设$\dim M\ge 3,$ 称$M$是逐点常截面曲率的, 若$M$上每点所有$2$-平面的截面曲率相同. 经典的Schur定理表示, 流形是逐点常截面曲率的当且仅当它是常截面曲率的. 证明利用了第二Bianchi恒等式.

本节只讨论了单连通的空间形式. 其它的空间形式从几何, 群论, 拓扑等观点考虑也都是很重要的. 它们的分类工作也是一个重要的课题.

文章最后更新于 2022-04-19 14:01:46