Machine-translated from Chinese.
回顾
对于Serre纤维化,
$$
E\xrightarrow{\pi} B,
$$
满足同伦提升性质(对CW复形).
若$B$是道路连通的, 纤维彼此都是同伦等价的, 记为
$$
F\rightarrow E\xrightarrow{\pi}B.
$$
定理 1. 令$F\rightarrow E\rightarrow B$为Serre纤维化, $B$单连通. 那么存在谱序列$E^r,$ $E^2_{p,q}=H_p(B;H_q(F)),$ 收敛到$E^\infty_{p,q}=G_pH_{p+q}(E).$
注 2. 若$\pi_1(B)\neq 0,$ 定理也成立, $H_\ast (B;H_\ast (F))$为具”局部系数”的同调, 由$\pi_1(B)$在$H_\ast (F)$上的作用表示. 若系数在域上选取, 则由万有系数定理与Kunneth公式, $E^2_{\ast ,\ast }=H_\ast (B;H_\ast (F))=H_\ast (B)\otimes H_\ast (F)=H_\ast (B\times F).$ $E^\infty=H_\ast (E).$ 同时$\dim H_n(B\times F)=\sum_{p+q=n} \dim E^2_{p,q}\ge \sum_{p+q=n} \dim E_{p,q}^\infty=\dim H_n(E).$ 这给出了对纤维丛同调维数的限制.
考虑$B$的CW逼近, 它与原纤维化弱同伦等价. 由于结论关于弱同伦等价不变,
不妨设$B$为CW复形. 取$B$的骨架滤列, 诱导了$E$上的滤列
$$
\cdots\subset \pi^{-1}(B^p)\subset \pi^{-1}(B^{p+1})\subset \cdots.
$$
进而我们有$C_\ast (E)$上的滤列, 取它的谱序列.
$$
E^0=G_pC_\ast (E)=C_\ast (\pi^{-1}(B^p),\pi^{-1}(B^{p-1})).
$$
$$
E^1_{p,q}=H_{p+q}(\pi^{-1}(B^p),\pi^{-1}(B^{p-1}))
$$
$(B^p,B^{p-1})$是$(p-1)$连通的,
$(\pi^{-1}(B^p),\pi^{-1}(B^{p-1}))$也是(通过长正合列).
因此$E^1_{p,q}$仅在$p,q\ge 0$时非平凡, 即在第一象限处.
接下来我们对$E^1$做简化:
$$
\begin{aligned}
E^1_{p,q}&\cong \bigoplus_{\substack{p-cells\\\sigma:D^p\rightarrow B} }H_{p+q}(\sigma^*E,(\sigma|_{S^{p-1} })^*E)\\
&\cong \bigoplus_{p-cells} H_q(F)\otimes H_p(D^p,S^{p-1})\\
&=C^{cell}_{p}(B;H_q(F))
\end{aligned}
$$
其中第一个同构关系由下图表示(具体细节暂略):
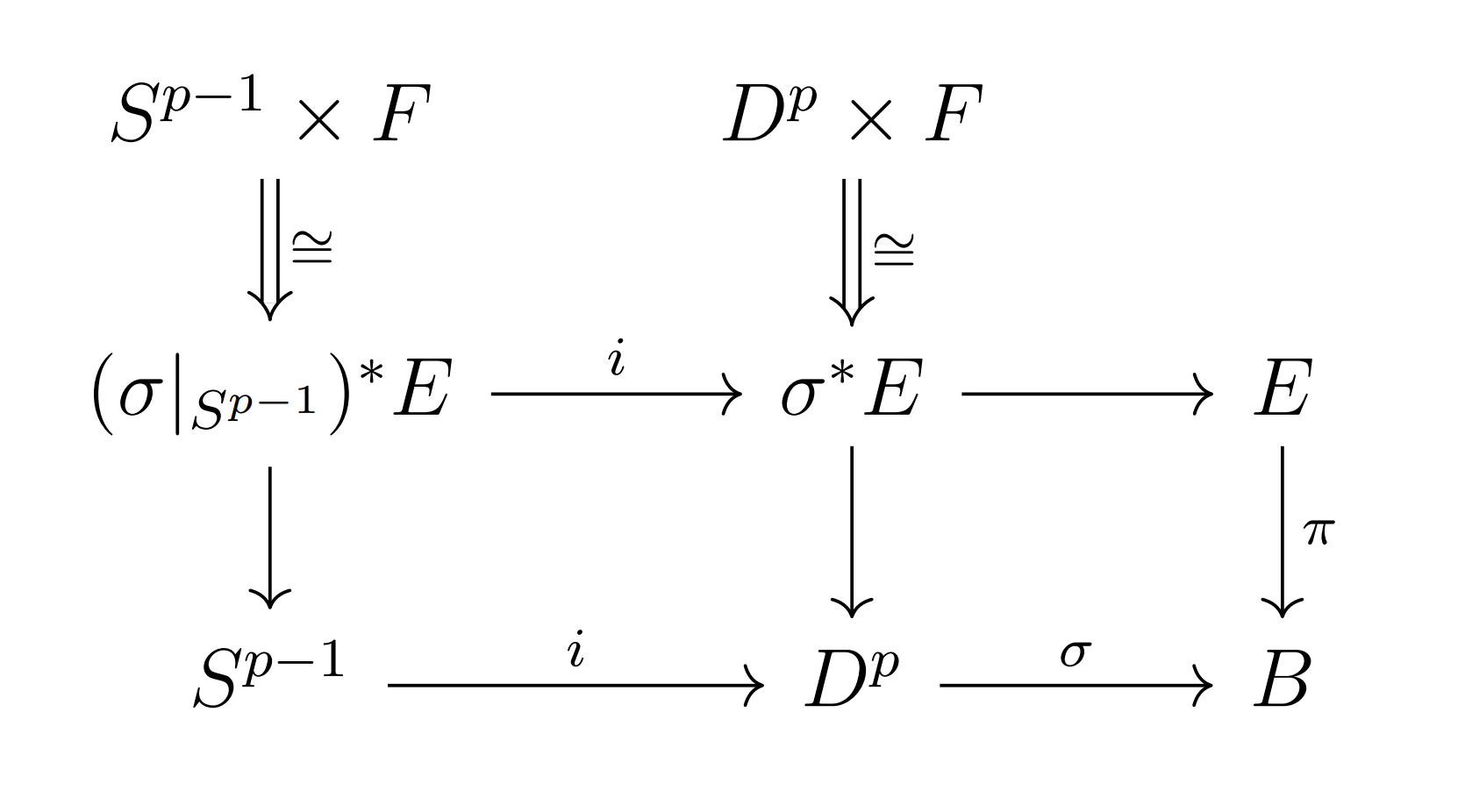
那么$\partial_1:E_{p,q}^1\rightarrow E_{p-1,q}^1$是胞腔复形上的微分.
$$
E^2_{p,q}=H_p^{cell}(B,H_q(F)).
$$
注 3. 谱序列的收敛性由谱序列仅在第一象限非平凡保证.
取纤维丛$U(1)\rightarrow U(2)\rightarrow S^3,$
$U(2)$可迁地作用在$S^3$上, $(1,0)$的稳定子同构于$U(1).$ $S^3=U(2)/U(1).$
我们有Leray-Serre谱序列:
$$
E^2_{p,q}=H_p(S^3;H_q(S^1))\cong H_p(S^3)\otimes H_q(S^1).
$$
此时谱序列从第二页开始就不再变化. 由于谱序列中只有一个平凡项,
$E^\infty=H_p(U(2))=\mathbb{Z},$ $p=0,1,2,3,$ 其余为零.
文章最后更新于 2022-09-22 19:38:54
review
For Serre fibrosis,
$$
E\xrightarrow{\pi} B,
$$
Satisfies the homotopy promotion property (for CW complex).
If $B$ is connected by roads, and the fibers are homotopic and equivalent to each other, it is recorded as
$$
F\rightarrow E\xrightarrow{\pi}B.
$$
Theorem 1. Let $F\rightarrow E\rightarrow B$ be Serre fibration, $B$ simply connected. Then there is a spectral sequence $E^r,$ $E^2_{p,q}=H_p(B;H_q(F)),$ that converges to $E^\infty_{p,q}=G_pH_{p+q}(E).$
Note 2. If the $\pi_1(B)\neq 0,$ theorem is also true, $H_\ast (B;H_\ast (F))$ is a homology with "local coefficient", represented by the effect of $\pi_1(B)$ on $H_\ast (F)$. If the coefficients are selected on the domain, then according to the universal coefficient theorem and Kunneth's formula, $E^2_{\ast ,\ast }=H_\ast (B;H_\ast (F))=H_\ast (B)\otimes H_\ast (F)=H_\ast (B\times F).$ $E^\infty=H_\ast (E).$ Also $\dim H_n(B\times F)=\sum_{p+q=n} \dim E^2_{p,q}\ge \sum_{p+q=n} \dim E_{p,q}^\infty=\dim H_n(E).$ this gives a limit on the homology dimension of fiber bundles.
Consider the CW approximation of $B$, which is equivalent to the fibrillation weak homotopy. Since the conclusion remains unchanged with respect to weak homotopy equivalence,
Let's assume $B$ is a CW complex. Take the skeleton filter sequence of $B$ and induce the filter sequence on $E$
$$
\cdots\subset \pi^{-1}(B^p)\subset \pi^{-1}(B^{p+1})\subset \cdots.
$$
Then we have the filtration on $C_\ast (E)$, and take its spectral sequence.
$$
E^0=G_pC_\ast (E)=C_\ast (\pi^{-1}(B^p),\pi^{-1}(B^{p-1})).
$$
$$
E^1_{p,q}=H_{p+q}(\pi^{-1}(B^p),\pi^{-1}(B^{p-1}))
$$
$(B^p,B^{p-1})$ is connected to $(p-1)$,
The same goes for $(\pi^{-1}(B^p),\pi^{-1}(B^{p-1}))$ (through long exact sequences).
Therefore $E^1_{p,q}$ is nontrivial only when $p,q\ge 0$, that is, in the first quadrant.
Next we simplify $E^1$:
$$
\begin{aligned}
E^1_{p,q}&\cong \bigoplus_{\substack{p-cells\\\sigma:D^p\rightarrow B} }H_{p+q}(\sigma^*E,(\sigma|_{S^{p-1} })^*E)\\
&\cong \bigoplus_{p-cells} H_q(F)\otimes H_p(D^p,S^{p-1})\\
&=C^{cell}_{p}(B;H_q(F))
\end{aligned}
$$
The first isomorphic relationship is represented by the following figure (the specific details are omitted for now):
Then $\partial_1:E_{p,q}^1\rightarrow E_{p-1,q}^1$ is the differential on the cell complex.
$$
E^2_{p,q}=H_p^{cell}(B,H_q(F)).
$$
Note 3. The convergence of the spectral sequence is guaranteed by the fact that the spectral sequence is non-trivial only in the first quadrant.
Get the fiber bundle $U(1)\rightarrow U(2)\rightarrow S^3,$
$U(2)$ can move on $S^3$, and the stabilizer of $(1,0)$ is isomorphic to $U(1).$ $S^3=U(2)/U(1).$
We have the Leray-Serre spectral sequence:
$$
E^2_{p,q}=H_p(S^3;H_q(S^1))\cong H_p(S^3)\otimes H_q(S^1).
$$
At this time, the spectral sequence will not change from the second page. Since there is only one trivial term in the spectral sequence,
$E^\infty=H_p(U(2))=\mathbb{Z},$ $p=0,1,2,3,$ The rest are zero.
The article was last updated on 2022-09-22 19:38:54
