《代数拓扑2》笔记(5)-上同调谱序列

基本概念

上同调谱序列和同调谱序列是类似的, 只是箭头都反了过来. 总的来说, 我们有:

• $R$模 $E_r^{p,q},$

• 微分$\delta_r:E_r^{p,q}\rightarrow E_r^{p+r,q-r+1},$

上链复形上滤列的包含关系将是反过来的, 即

$$F_pC^\ast \supset F_{p+1}C^\ast .$$

这就给出了谱序列$(E_r^{p,q},\delta_r),$ $E_1^{p,q}=H^{p+q}(G_pC^\ast ).$ 谱序列收敛到$E_\infty^{p,q}=G_pH^{p+q}(C^\ast )$若滤列对每个$C^i$有界.

乘法结构

设$(C^\ast ,\delta)$有一个乘法结构(本身满足运算律如结合律等),

$$\cup:C^i\otimes C^j\rightarrow C^{i+j},$$

我们希望它与微分和滤列兼容, 这样它就可以放到谱序列上.

与微分的兼容性要求它是导子:

$$\delta(\alpha\cup \beta)=(\delta\alpha)\cup \beta+(-1)^i\alpha\cup(\delta\beta),\quad \alpha\in C^i.$$

与滤列的兼容性要求:

$$\cup:F_pC^\ast \otimes F_{p'}C^\ast \rightarrow F_{p+p'}C^\ast .$$

这样$\cup$便(归纳地)诱导了一个谱序列上良定的乘法:

$$\cup_r:E_r^{p,q}\otimes E_r^{p',q'}\rightarrow E_r^{p+p',q+q'}.$$

命题 1. $\delta_r$是$E_r^{p,q}$上的一个导子, 即:

$$\delta_r(\alpha\cup_r \beta)=(\delta_r\alpha)\cup_r\beta+(-1)^{|\alpha|}\alpha\cup_r(\delta_r\beta),\quad |\alpha|:=p+q,\quad \alpha\in E_r^{p,q}.$$

命题 2. 若滤列对每个$C^i$有界, 那么$E_\infty^{p,q}$上的乘法结构与$G_pH^{p+q}(C^\ast )$上自然的乘法结构相容.

我们说$E_r$是一个代数谱序列, 若它有一个乘法结构.

Leray-Serre上同调谱序列

对于Serre纤维化, $B$道路连通,

$$F\rightarrow E\xrightarrow{\pi} B$$

对于交换环$R,$ $H^\ast (F;R)$是一个(分级交换)$R$代数, $E_2^{p,q}=H^p(B;H^q(F;R))$是一个$R$代数, $E_r$是一个代数谱序列, $E_\infty^{p,q}=G_pH^{p+q}(E;R).$

注 3. 若$\cup$表示$H^\ast (B;H^\ast (F;R))$上的标准乘法结构, $\cup_2$是$E_2^{p,q}$上的乘法结构, 那么

$$\alpha\cup_2\alpha'=(-1)^{qp'}\alpha\cup\alpha',\quad \alpha\in E_2^{p,q},\alpha'\in E_2^{p',q'}.$$

我们的目标是让$(E_r,\delta_r,\cup_r)$成为微分分级代数, 使得有

$$\alpha\beta=(-1)^{|\alpha||\beta|}\beta\alpha,$$ $$\delta(\alpha\beta)=(\delta \alpha)\beta+(-1)^{|\alpha|}\alpha(\delta\beta).$$

定理 4. $H^\ast (SU(n))\cong \Lambda^\ast (a_3,a_5,\cdots,a_{2k-1})$为代数同构(后者为外代数).

用归纳法. $n=1$平凡. 对$n\ge 2,$ 考虑

$$SU(n-1)\rightarrow SU(n)\rightarrow S^{2n-1},$$

考虑它的构造. $SU(n)$可迁地作用在$S^{2n-1}\subset \mathbb{C}^n$上, $(1,0,\cdots,0)$的稳定子就是$SU(n-1).$ 从而$S^{2n-1}\cong \frac{SU(n)}{SU(n-1)}.$

考虑Leray-Serre谱序列,

$$E_2=H^\ast (S^{2n-1};H^\ast (SU(n-1)))\cong H(S^{2n-1})\otimes H^\ast (SU(n-1)).$$

谱序列如下图所示, 唯一一个可能非零的$\delta_{2n-1}$由导子性质也是零(通过分解). 从而谱序列从$E_2$开始就停止.

$$E_\infty=E_2=H^\ast (S^{2n-1})\otimes \Lambda^\ast (a_3,\cdots,a_{2n-3})=\Lambda^\ast (a_3,\cdots,a_{2n-1}).$$

新加的生成元对应于$H^{2n-1}(S^{2n-1})$的生成元.

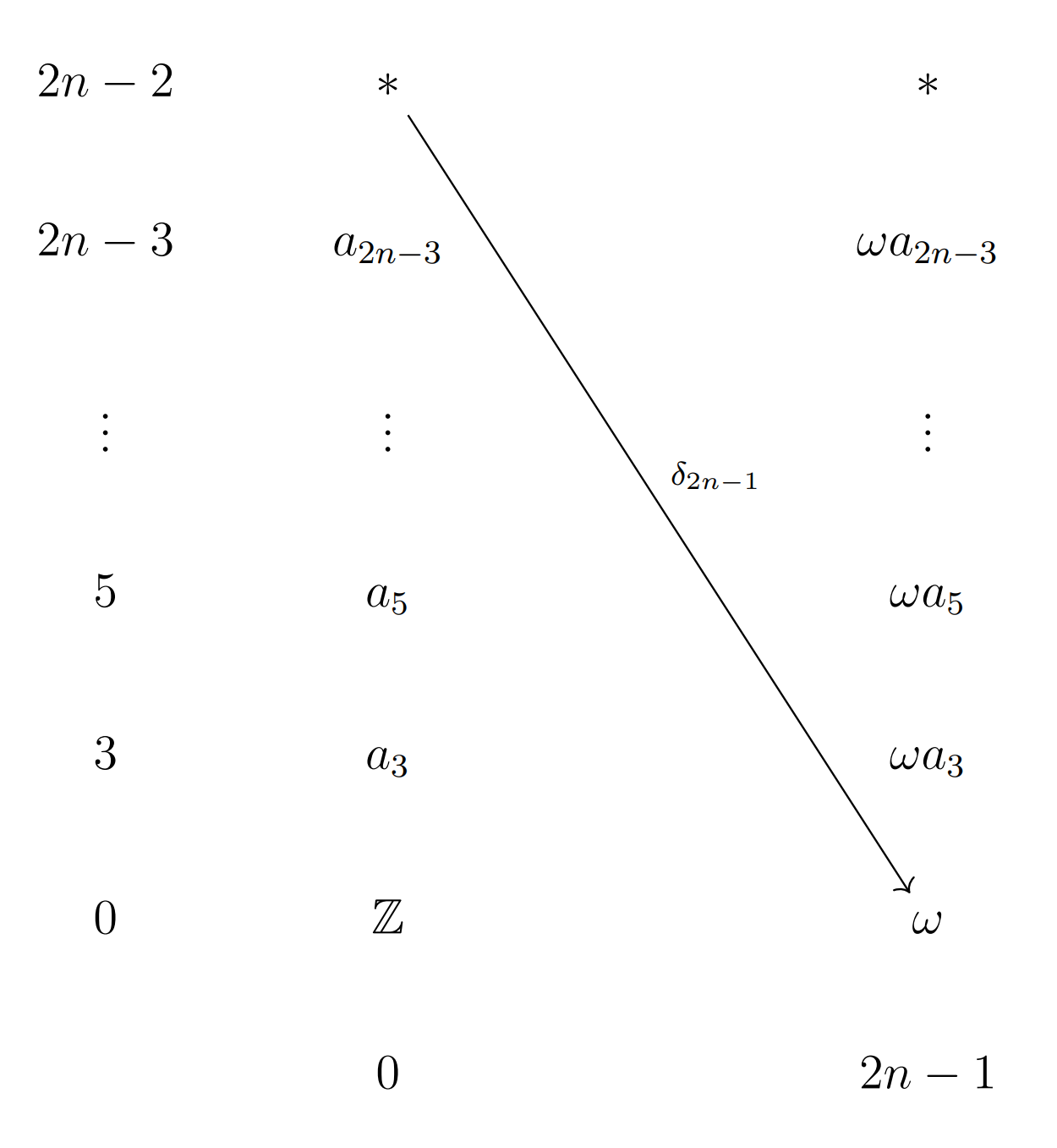
注意到$\Lambda^\ast (a_3,\cdots,a_{2n-1})$是一个自由代数, 延展问题是平凡的, 从而

$$\bigoplus_i H^i(SU(n))\cong \bigoplus_i\bigoplus_pG_pH^i(SU(n))=\bigoplus_i\bigoplus_p E_{\infty}^{p,i-p}.$$

定理 5. 若$E_\infty$是自由的分级交换双分级代数, 那么$H^\ast \cong E_\infty$为代数同构.

边同态

假设$E_2\Rightarrow H^\ast $为第一象限, 那么

$$E_\infty^{0,q}\hookrightarrow \cdots \hookrightarrow E_3^{0,q}\hookrightarrow E_2^{0,q}$$ $$E_2^{p,0}\twoheadrightarrow E_3^{p,0}\twoheadrightarrow \cdots\twoheadrightarrow E_\infty^{p,0}$$

进一步,

$$E_\infty^{0,q}=G_0H^q=\frac{F_0H^q}{F_1H^q},\quad H^q\twoheadrightarrow E_\infty^{0,q};$$ $$E_\infty^{p,0}=G_pH^p=\frac{F_pH^p}{F_{p+1}H^p=0}, \quad E_\infty^{p,0}\hookrightarrow H^p.$$

可以定义边同态研究两者的关系.

文章最后更新于 2022-09-29 16:15:30