Machine-translated from Chinese.
上同调的Leray-Serre谱序列
一些不加说明的具体构造过程如下所示:
$$
F\rightarrow E\xrightarrow{\pi}B,
$$
$$
\cdots \subset B^p\subset B^{p+1}\subset \cdots,
$$
$$
E^p:=\pi^{-1}(B^p),
$$
$$
\cdots\subset E^p \subset E^{p+1}\subset\cdots,
$$
$$
F_pC_\ast (E):=C_\ast (E^p),\quad F_pC^\ast (E):=\operatorname{Ann}(F_{p-1}C_\ast )=\{f:f|_{F_{p-1}C_\ast }=0\}\subset \operatorname{Hom}(C_\ast ;R).
$$
$F_pC^\ast (E)$是$C^\ast (E)$上的一列递减滤列. 从而构造谱序列.
边同态
在第一象限, 我们有自然的映射列:
$$
E_\infty^{0,q}\hookrightarrow\cdots\hookrightarrow E_3^{0,q}\hookrightarrow E_2^{0,q}
$$
$$
E_2^{p,0}\twoheadrightarrow{E_3^{p,0} }\twoheadrightarrow\cdots \twoheadrightarrow E_\infty^{p,0}
$$
那么,
$$
E_\infty^{0,q}=G_0H^q,\quad H^q\twoheadrightarrow{E_\infty^{0,q} }
$$
$$
E_\infty^{p,0}=G_pH^p,\quad E_\infty^{p,0}\hookrightarrow H^p.
$$
用上面映射的复合定义边同态:
$$
H^q\twoheadrightarrow E_\infty^{0,q} \hookrightarrow E_2^{0,q},
$$
$$
E_2^{p,0}\twoheadrightarrow E_\infty^{p,0}\hookrightarrow H^p
$$
考虑谱序列
$$
F\xrightarrow{\iota}E\xrightarrow{\pi}B,
$$
$F$连通,
$B$单连通. 那么边同态
$$
H^q(E;R)\twoheadrightarrow E_\infty^{0,q}\hookrightarrow E_2^{0,q}= H^0(B;H^q(F;R))=H^q(F;R).
$$
是$\iota^\ast =H^q(\iota).$ 若$\iota^\ast $是满射, 那么上行的嵌入也是满射,
从而是同构, 得到谱序列的信息.
$$
H^p(B;R)=H^p(B;H^0(F,R))=E_2^{p,0}\twoheadrightarrow E_\infty^{p,0} \hookrightarrow H^p(E;R)
$$
是$\pi^\ast =H^p(\pi).$ 若$\pi^\ast $是单射, 那么上行的满射是同构.
Leray-Hirsch定理
定理 1. 对于纤维化$F\xrightarrow{\iota}E\xrightarrow{\pi}B,$ $B$道路连通. 若$\iota^\ast :H^q(E)\rightarrow H^q(F)$是满射, $\,\forall\,q,$ 且$H^\ast (F)$是有限生成自由Abel群, 那么$H^\ast (E)\cong H^\ast (B)\otimes H^\ast (F)$作为$H^\ast (B)$模同构.
证明思路: 满射的条件给出$\pi_1(B)$在$H^\ast (F)$上的作用是平凡的.
而有限生成自由Abel的条件说明了
$$
E_2^{p,q}=H^p(B;H^q(F))\cong H^p(B)\otimes H^q(F).
$$
由于边上的微分都是零, 由微分的导子性质, 所有地方的微分都是零.
这就立刻得到了谱序列从第二页开始就不再变化, 从而收敛得到结论.
若我们能够找到$\iota,\pi$对应的截面,
那么立即有$\iota^\ast ,\pi^\ast $是满射/单射.
Hurewicz定理及其推广
定理 2 (Hurewicz). 设$X$是单连通的, 那么$\pi_i(X)=0,$ $\,\forall\,i<n$ 当且仅当$\widetilde{H}_i(X)=0,$ $\,\forall\,i<n.$ 若条件满足, 那么$\pi_n(X)\cong H_n(X).$
对$n$归纳, 考虑道路纤维化:
$$
\Omega X\rightarrow PX\rightarrow X
$$
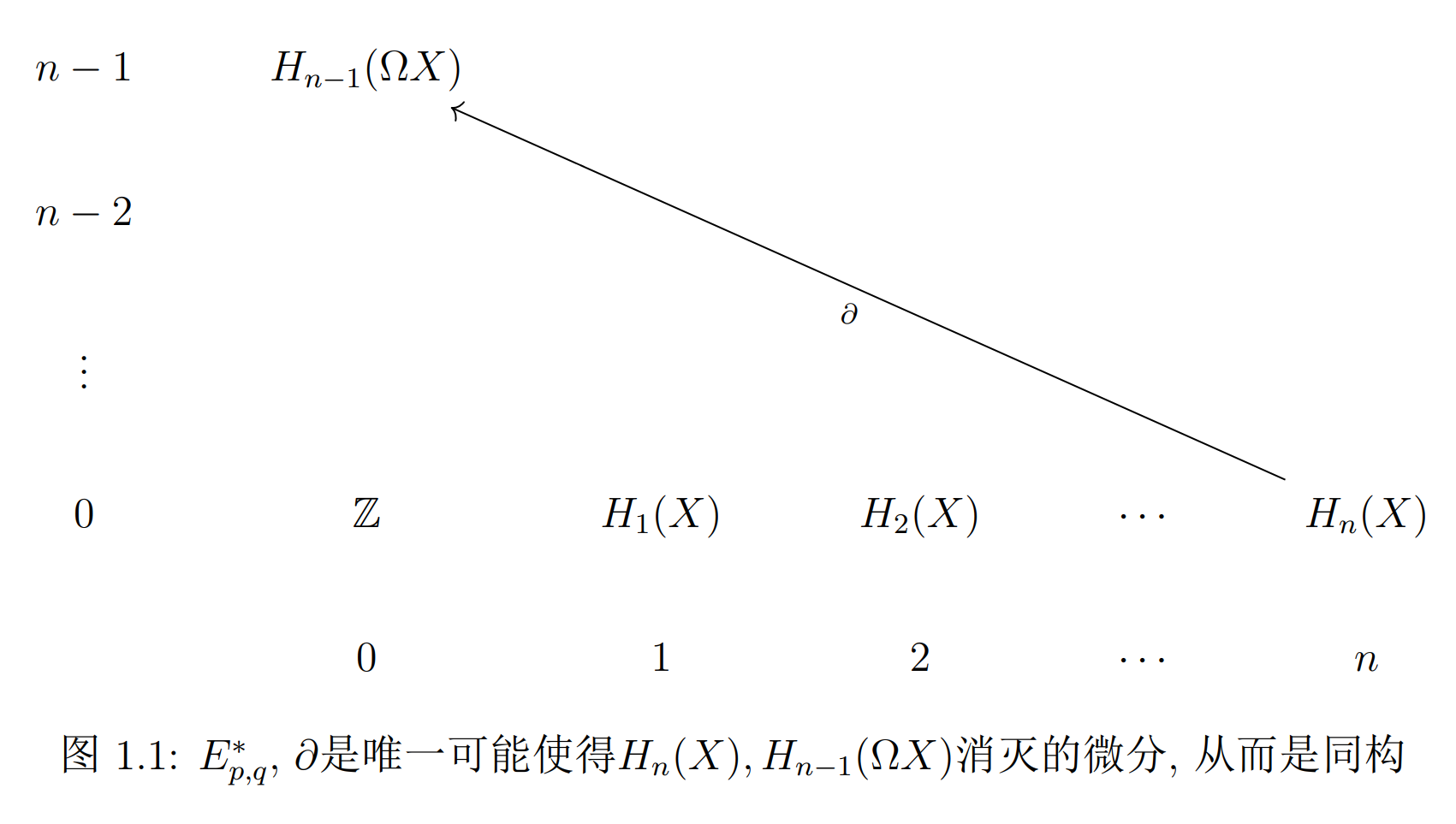
其中$\Omega X$是环空间, $PX$是道路空间, 可缩. $\,\forall\,q<n-1,$
由归纳假设,
$$
0=\pi_{q+1}(X)\cong \pi_q(\Omega X)\cong H_q(\Omega X).
$$
$$
\pi_n(X)\cong \pi_{n-1}(\Omega X)\cong H_{n-1}(\Omega X).
$$
我们的目标是关联$H_\ast (\Omega X),$ $H_\ast (X).$
由Leray-Serre谱序列, $E^2_{p,q}=H_p(X;H_q(\Omega X)),$ 但由于$PX$可缩,
$E^\infty_{p,q}=0$除了$E^\infty_{0,0}.$
也就是$E^2_{p,q}$上所有元素都会被消灭(除了$(0,0)$).
那么由下面的谱序列立即得到结论.
Serre类
Serre类$\mathscr{C}$是一个由Abel群组成的非空集, 使得对任意短正合列
$$
0\rightarrow A\rightarrow B \rightarrow C\rightarrow 0,
$$
$B\in \mathscr{C}$当且仅当$A,C\in \mathscr{C}.$
我们称$\mathscr{C}$是”好”的, 若
$$
\,\forall\,A,B\in \mathscr{C},\quad A\otimes B,\operatorname{Tor}(A,B)\in \mathscr{C}.
$$
几个例子是: $\{0\}$,{挠Abel群(每个元素阶有限)}, {有限Abel群}.
{有限生成Abel群}, {$p$群(每个元素阶为$p^n$)}.
我们定义$f:A\rightarrow B$是$\mathscr{C}$单射若$\ker f\in \mathscr{C};$
称它是$\mathscr{C}$满射, 若$\operatorname{coker}f\in \mathscr{C}.$
称它是$\mathscr{C}$同构若满足以上两个条件.
定理 3 (推广Hurewicz). 令$X$是单连通的, $\mathscr{C}$是好Serre类. 那么$\pi_i(X)\in \mathscr{C},$ $\,\forall\,i<n$ 当且仅当$\widetilde{H}_i(X)\in \mathscr{C},$ $\,\forall\,i<n.$ 若条件成立, $\pi_n(X)\rightarrow H_n(X)$是$\mathscr{C}$同构.
证明思路: 对$n$归纳.
$$
\,\forall\,q<n-1, \quad \mathscr{C}\ni \pi_{q+1}(X)\cong_\mathscr{C}H_q(\Omega X),\qquad \pi_n(X)\cong_\mathscr{C}H_{n-1}(\Omega X).
$$
$$
E^2_{p,q}=H_p(X;H_q(\Omega X)),\quad H_{\ast }(PX)=H_{\ast }(\ast )
$$
从而由$H_q(\Omega X)\in \mathscr{C},$ $E^2_{p,q}\in \mathscr{C}.$
再次由谱序列得到结论.
推论 4. 若$X$是单连通有限CW复形, 那么$\pi_i(X)$是有限生成的, $\,\forall\,i.$
注 5. $\pi_2(S^1\vee S^2)$并不是有限生成的.
文章最后更新于 2022-10-03 17:32:02
Cohomological Leray-Serre spectral sequence
Some specific construction processes without explanation are as follows:
$$
F\rightarrow E\xrightarrow{\pi}B,
$$
$$
\cdots \subset B^p\subset B^{p+1}\subset \cdots,
$$
$$
E^p:=\pi^{-1}(B^p),
$$
$$
\cdots\subset E^p \subset E^{p+1}\subset\cdots,
$$
$$
F_pC_\ast (E):=C_\ast (E^p),\quad F_pC^\ast (E):=\operatorname{Ann}(F_{p-1}C_\ast )=\{f:f|_{F_{p-1}C_\ast }=0\}\subset \operatorname{Hom}(C_\ast ;R).
$$
$F_pC^\ast (E)$ is a descending filter sequence on $C^\ast (E)$. Thus, a spectral sequence is constructed.
edge homomorphism
In the first quadrant, we have the natural mapping columns:
$$
E_\infty^{0,q}\hookrightarrow\cdots\hookrightarrow E_3^{0,q}\hookrightarrow E_2^{0,q}
$$
$$
E_2^{p,0}\twoheadrightarrow{E_3^{p,0} }\twoheadrightarrow\cdots \twoheadrightarrow E_\infty^{p,0}
$$
Then,
$$
E_\infty^{0,q}=G_0H^q,\quad H^q\twoheadrightarrow{E_\infty^{0,q} }
$$
$$
E_\infty^{p,0}=G_pH^p,\quad E_\infty^{p,0}\hookrightarrow H^p.
$$
Define edge homomorphisms using the composition of the mapping above:
$$
H^q\twoheadrightarrow E_\infty^{0,q} \hookrightarrow E_2^{0,q},
$$
$$
E_2^{p,0}\twoheadrightarrow E_\infty^{p,0}\hookrightarrow H^p
$$
Consider the spectral sequence
$$
F\xrightarrow{\iota}E\xrightarrow{\pi}B,
$$
$F$ Connected,
$B$ Simply connected. Then edge homomorphism
$$
H^q(E;R)\twoheadrightarrow E_\infty^{0,q}\hookrightarrow E_2^{0,q}= H^0(B;H^q(F;R))=H^q(F;R).
$$
is $\iota^\ast =H^q(\iota).$. If $\iota^\ast $ is surjective, then the uplink embedding is also surjective,
Therefore, it is isomorphism, and the information of the spectral sequence is obtained.
$$
H^p(B;R)=H^p(B;H^0(F,R))=E_2^{p,0}\twoheadrightarrow E_\infty^{p,0} \hookrightarrow H^p(E;R)
$$
is $\pi^\ast =H^p(\pi).$. If $\pi^\ast $ is an injective, then the upward surjection is isomorphism.
Leray-Hirsch theorem
Theorem 1. For fibrotic $F\xrightarrow{\iota}E\xrightarrow{\pi}B,$ $B$ roads are connected. If $\iota^\ast :H^q(E)\rightarrow H^q(F)$ is a surjection, $\,\forall\,q,$ and $H^\ast (F)$ are a finitely generated free Abel group, then $H^\ast (E)\cong H^\ast (B)\otimes H^\ast (F)$ serves as the $H^\ast (B)$ module isomorphism.
Proof idea: The surjective condition gives that the effect of $\pi_1(B)$ on $H^\ast (F)$ is trivial.
The conditions for finitely generated free Abel illustrate
$$
E_2^{p,q}=H^p(B;H^q(F))\cong H^p(B)\otimes H^q(F).
$$
Since the differentials on the edges are all zero, due to the derivative properties of differentials, the differentials everywhere are zero.
This immediately leads to the conclusion that the spectrum sequence will not change from the second page, thus converging.
If we can find the section corresponding to $\iota,\pi$,
Then immediately $\iota^\ast ,\pi^\ast $ is surjective/injective.
Hurewicz's theorem and its extension
Theorem 2 (Hurewicz). Assume $X$ is simply connected, then $\pi_i(X)=0,$ $\,\forall\,i<n$ if and only if $\widetilde{H}_i(X)=0,$ $\,\forall\,i<n.$ If the conditions are met, then $\pi_n(X)\cong H_n(X).$
Generalize $n$ and consider road fibrosis:
$$
\Omega X\rightarrow PX\rightarrow X
$$
Where $\Omega X$ is the ring space, $PX$ is the road space, which is shrinkable. $\,\forall\,q<n-1,$
By the inductive hypothesis,
$$
0=\pi_{q+1}(X)\cong \pi_q(\Omega X)\cong H_q(\Omega X).
$$
$$
\pi_n(X)\cong \pi_{n-1}(\Omega X)\cong H_{n-1}(\Omega X).
$$
Our goal is to associate $H_\ast (\Omega X),$ $H_\ast (X).$
From the Leray-Serre spectral sequence, $E^2_{p,q}=H_p(X;H_q(\Omega X)),$ but since $PX$ is contractible,
$E^\infty_{p,q}=0$ except $E^\infty_{0,0}.$
That is, all elements on $E^2_{p,q}$ will be destroyed (except $(0,0)$).
Then the conclusion can be drawn immediately from the following spectral sequence.
Serre class
The Serre class $\mathscr{C}$ is a non-empty set consisting of Abelian groups such that for any short exact sequence
$$
0\rightarrow A\rightarrow B \rightarrow C\rightarrow 0,
$$
$B\in \mathscr{C}$ if and only if $A,C\in \mathscr{C}.$
We call $\mathscr{C}$ "good" if
$$
\,\forall\,A,B\in \mathscr{C},\quad A\otimes B,\operatorname{Tor}(A,B)\in \mathscr{C}.
$$
A few examples are: $\{0\}$, {Abelian group (each element is of finite order)}, {Finite Abelian group}.
{Finitely generated Abel group}, {$p$ group (each element is of order $p^n$)}.
We define $f:A\rightarrow B$ to be $\mathscr{C}$ injective if $\ker f\in \mathscr{C};$
Call it a $\mathscr{C}$ surjection, if $\operatorname{coker}f\in \mathscr{C}.$
It is called $\mathscr{C}$ isomorphism if it satisfies the above two conditions.
Theorem 3 (Promoting Hurewicz). Let $X$ be simply connected, $\mathscr{C}$ be a good Serre class. Then $\pi_i(X)\in \mathscr{C},$ $\,\forall\,i<n$ if and only if $\widetilde{H}_i(X)\in \mathscr{C},$ $\,\forall\,i<n.$ If the condition is true, $\pi_n(X)\rightarrow H_n(X)$ is isomorphic to $\mathscr{C}$.
Proof idea: Induction on $n$.
$$
\,\forall\,q<n-1, \quad \mathscr{C}\ni \pi_{q+1}(X)\cong_\mathscr{C}H_q(\Omega X),\qquad \pi_n(X)\cong_\mathscr{C}H_{n-1}(\Omega X).
$$
$$
E^2_{p,q}=H_p(X;H_q(\Omega X)),\quad H_{\ast }(PX)=H_{\ast }(\ast )
$$
Thus $H_q(\Omega X)\in \mathscr{C},$ $E^2_{p,q}\in \mathscr{C}.$
The conclusion is drawn again from the spectral sequence.
Corollary 4. If $X$ is a simply connected finite CW complex, then $\pi_i(X)$ is finitely generated, $\,\forall\,i.$
Note 5. $\pi_2(S^1\vee S^2)$ is not finitely generated.
The article was last updated on 2022-10-03 17:32:02
